Published online by Cambridge University Press: 11 May 2021
Stable accessibility of partially hyperbolic systems is central to their stable ergodicity, and we establish its
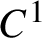 $C^1$
-density among partially hyperbolic flows, as well as in the categories of volume-preserving, symplectic, and contact partially hyperbolic flows. As applications, we obtain on one hand in each of these four categories of flows the
$C^1$
-density among partially hyperbolic flows, as well as in the categories of volume-preserving, symplectic, and contact partially hyperbolic flows. As applications, we obtain on one hand in each of these four categories of flows the
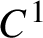 $C^1$
-density of the
$C^1$
-density of the
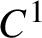 $C^1$
-stable topological transitivity and triviality of the centralizer, and on the other hand the
$C^1$
-stable topological transitivity and triviality of the centralizer, and on the other hand the
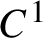 $C^1$
-density of the
$C^1$
-density of the
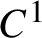 $C^1$
-stable K-property of the natural volume in the latter three categories.
$C^1$
-stable K-property of the natural volume in the latter three categories.
To the memory of Anatole Katok