Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T20:31:54.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Absolutely continuous invariant measures for piecewise expanding C2 transformations in Rn on domains with cusps on the boundaries

Published online by Cambridge University Press:  19 September 2008

Kourosh Adl-Zarabi
Kourosh Adl-Zarabi
Affiliation:
Department of Mathematics and Statistics, Concordia University, 7141 Sherbrooke St West, Montreal, CanadaH4B 1R6 (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

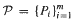Let Ω be a bounded region in Rn and let be a partition of Ω into a finite number of subsets having piecewise C2 boundaries. The boundaries may contain cusps. Let τ: Ω → Ω be piecewise C2 on 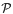and expanding in the sense that there exists α > 1 such that for any i = 1, 2,…,m, 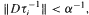where 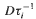is the derivative matrix of 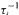and ‖·‖ is the euclidean matrix norm. The main result provides a lower bound on α which guarantees the existence of an absolutely continuous invariant measure for τ.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 16 , Issue 1 , February 1996 , pp. 1 - 18
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Li, T.-Y. and Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186 (1973), 481–488.Google Scholar
[2]Keller, G.. Ergodicite et mesures invariantes pour les transformations dilatantes par morcaux d'une region bornee du plan. C. R. Acad. Sri. Paris 289 Serie A (1979), 625–627.Google Scholar
[3]Keller, G.. Proprietes ergerdiques des endomorphismes dilatants, C 2 par morceaux, des regions bornees du plan. Thesis, Universite de Rennes (1979).Google Scholar
[4]Giusti, E.. Minimal Surfaces and Functions of Bounded Variation. Birkhäuser, Boston, 1984.CrossRefGoogle Scholar
[5]Góra, P. and Boyarsky, A.. Absolutely continuous invariant measures for piecewise expanding C 2 transformations in RN. Israel J. Math. 67(3) (1989), 272–276.CrossRefGoogle Scholar
[6]Jabloński, M.. On invariant measures for piecewise C 2 transformations of the n-dimensional cube. Ann. Polon. Math. XLIII (1983), 185–195.CrossRefGoogle Scholar
[7]Ivanov, V. V. and Kachurowski, A. G.. Absolutely continuous invariant measures for locally expanding transformations. Preprint No. 27. Institute of Mathematics AN USSR, Siberian Section (in Russianp).Google Scholar
[8]Candeloro, D.. Misure invariante per transformazioni in piu dimensioni. Atti Sem. Mat. Fis. Univ. Moena XXXV (1987), 33–42.Google Scholar
[9]Krzyzewski, K. and Szlenk, W.. On invariant measures for expanding differentiable mappings. Studia Math. 33 (1969), 82–92.CrossRefGoogle Scholar
[10]Straube, E.. On the existence of invariant absolutely continuous measures. Commun. Math. Phys. 81 (1981), 27–30.CrossRefGoogle Scholar
[11]Kosyakin, A. A. and Sandier, E. A.. Ergodic properties of a class of piecewise-smooth transformations of an interval. Izv. VUZ Matematika 3[118] (1972), 32–40. (English translation from the British Library, Translation Service.)Google Scholar
[12]Kosyakin, A. A. and Sandier, E. A.. Stochasticity of a certain class of discrete system. Translated from Automatika and Telemekhanika No. 9 (1972), 87–92.Google Scholar
[13]Schweiger, F.. Invariant Measures and Ergodic Properties of Numbertheoretical Endomorphisms. Banach Center Publications, vol. 23, pp. 283–295. PWN-Polish Scientific Publishers, Warszawa.Google Scholar
[14]Lasota, A. and Mackey, M.. Probabilistic Properties of Deterministic Systems. Cambridge University Press, Cambridge, 1985.CrossRefGoogle Scholar
[15]Yuri, M.. On a Bernouilli property for multi-dimensional mappings with finite range structure. In: Dynamical Systems and Nonlinear Oscillations, Vol. 1. Ikegami, Giko, ed. World Scientific, Singapore, 1986.Google Scholar
[16]Tulcea, C. T. Ionescu and Marinescu, G.. Theorie ergodique pour des classes d'operations non completement continues. Ann. Math. 52 (1950), 140–147.CrossRefGoogle Scholar
[17]Adl-Zarabi, K.. Absolutely continuous invariant measures for higher dimensional expanding transformations. Ph.D. Thesis, Conordia University, Montreal Canada.Google Scholar