Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T04:33:46.506Z Has data issue: false hasContentIssue false
  • English
  • Français

When are all closed subsets recurrent?

Published online by Cambridge University Press:  12 May 2016

JIE LI ,
PIOTR OPROCHA ,
XIANGDONG YE  and
RUIFENG ZHANG
JIE LI
Affiliation:
Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Sciences, Hefei, Anhui 230026, PR China School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, PR China email [email protected], [email protected]
PIOTR OPROCHA
Affiliation:
AGH University of Science and Technology, Faculty of Applied Mathematics, al. A. Mickiewicza 30, 30-059 Kraków, Poland National Supercomputing Centre IT4Innovations, Division of the University of Ostrava, Institute for Research and Applications of Fuzzy Modeling, 30. dubna 22, 70103 Ostrava, Czech Republic email [email protected]
XIANGDONG YE
Affiliation:
Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Sciences, Hefei, Anhui 230026, PR China School of Mathematical Sciences, University of Science and Technology of China, Hefei, Anhui 230026, PR China email [email protected], [email protected]
RUIFENG ZHANG
Affiliation:
School of Mathematics, Hefei University of Technology, Hefei, Anhui 230009, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

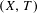In the paper we study relations of rigidity, equicontinuity and pointwise recurrence between an invertible topological dynamical system (t.d.s.) $(X,T)$ and the t.d.s. 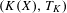$(K(X),T_{K})$ induced on the hyperspace 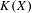$K(X)$ of all compact subsets of 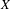$X$, and provide some characterizations. Among other examples, we construct a minimal, non-equicontinuous, distal and uniformly rigid t.d.s. and a weakly mixing t.d.s. which induces dense periodic points on the hyperspace 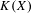$K(X)$ but itself does not have dense distal points, solving in that way a few open questions from earlier articles by Dong, and Li, Yan and Ye.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 7 , October 2017 , pp. 2223 - 2254
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E., Auslander, J. and Berg, K.. When is a transitive map chaotic? Convergence in Ergodic Theory and Probability. Walter de Gruyter, Berlin, 1996, pp. 25–40.Google Scholar
Akin, E., Auslander, J. and Glasner, E.. The topological dynamics of Ellis actions. Mem. Amer. Math. Soc. 195 (2008), vi+152pp.Google Scholar
Akin, E., Auslander, J. and Nagar, A.. Dynamics of induced systems. Preprint, 2014, arXiv:1412.2388.Google Scholar
Auslander, J.. Minimal Flows and Their Extensions. North-Holland, Amsterdam, 1988.Google Scholar
Auslander, J., Glasner, E. and Weiss, B.. On recurrence in zero dimensional flows. Forum Math. 19 (2007), 107–114.CrossRefGoogle Scholar
Banks, J.. Chaos for induced hyperspace maps. Chaos Solitons Fractals 25 (2005), 681–685.Google Scholar
Bauer, W. and Sigmund, K.. Topological dynamics of transformations induced on the space of probability measures. Monatsh. Math. 79 (1975), 81–92.CrossRefGoogle Scholar
Blanchard, F.. A disjointness theorem involving topological entropy. Bull. Soc. Math. France 121 (1993), 465–478.CrossRefGoogle Scholar
Blanchard, F., Host, B. and Ruette, S.. Asymptotic pairs in positive-entropy systems. Ergod. Th. & Dynam. Sys. 22 (2002), 671–686.Google Scholar
Block, L. S. and Coppel, W. A.. Dynamics in One Dimension (Lecture Notes in Mathematics, 1513) . Springer, Berlin, 1992.CrossRefGoogle Scholar
Brin, M. and Stuck, G.. Introduction to Dynamical Systems. Cambridge University Press, Cambridge, 2003.Google Scholar
Dong, P.. Recurrence, disjointness, independence and related problems with nilsystems. PhD Thesis, USTC, 2012.Google Scholar
Dong, P., Shao, S. and Ye, X.. Product recurrent properties, disjointness and weak disjointness. Israel J. Math. 188 (2012), 463–507.Google Scholar
Falniowski, F., Kulczycki, M., Kwietniak, D. and Li, J.. Two results on entropy, chaos, and independence in symbolic dynamics. Discrete Contin. Dyn. Syst. Ser. B 20(10) (2015), 3487–3505.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.Google Scholar
Glasner, E. and Weiss, B.. Sensitive dependence on initial conditions. Nonlinearity 6 (1993), 1067–1075.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. Quasi-factors of zero-entropy systems. J. Amer. Math. Soc. 8 (1995), 665–686.Google Scholar
Glasner, S. and Maon, D.. Rigidity in topological dynamics. Ergod. Th. & Dynam. Sys. 9 (1989), 309–320.CrossRefGoogle Scholar
Gottschalk, W. H.. Characterization of almost periodic transformation groups. Proc. Amer. Math. Soc. 7 (1956), 709–712.Google Scholar
Gottschalk, W. H. and Hedlund, G. A.. Topological Dynamics. American Mathematical Society, Providence, RI, 1955.Google Scholar
Halmos, P. R. and Von Neumann, J.. Operator methods in classical mechanics, II. Ann. of Math. (2) 43 (1942), 332–350.CrossRefGoogle Scholar
Hochman, M.. On notions of determinism in topological dynamics. Ergod. Th. & Dynam. Sys. 32 (2011), 119–140.Google Scholar
Huang, W. and Ye, X.. Topological complexity, return times and weak disjointness. Ergod. Th. & Dynam. Sys. 24 (2004), 825–846.Google Scholar
Huang, W. and Ye, X.. Dynamical systems disjoint from any minimal system. Trans. Amer. Math. Soc. 357 (2005), 669–694.Google Scholar
Huang, W. and Ye, X.. A local variational relation and applications. Israel J. Math. 151 (2006), 237–279.CrossRefGoogle Scholar
Illanes, A. and Nadler, S. B. Jr. Hyperspaces. Fundamentals and Recent Advances (Monographs and Textbooks in Pure and Applied Mathematics, 216) . Marcel Dekker, New York, 1999.Google Scholar
Katznelson, Y. and Weiss, B.. When all points are recurrent/generic. Progress in Mathematics, Vol. 10 (Proceedings of Special Year, Maryland 1979–1980). Birkhauser, Boston, MA, 1981, pp. 195–210.Google Scholar
Kerr, D. and Li, H.. Independence in topological and C∗ -dynamics. Math. Ann. 338 (2007), 869–926.CrossRefGoogle Scholar
Korner, T. W.. Recurrence without uniform recurrence. Ergod. Th. & Dynam. Sys. 7 (1987), 559–566.CrossRefGoogle Scholar
Kuratowski, K.. Topology. PWN – Polish Scientific Publishers, Warszawa, 1968, I.Google Scholar
Kuratowski, K. and Mostowski, A.. Set Theory. PWN – Polish Scientific Publishers, Warsaw, 1968, North-Holland, Amsterdam.Google Scholar
Li, J.. Equivalent conditions of Devaney chaos on the hyperspace. J. Univ. Sci. Technol. China 44 (2014), 93–95.Google Scholar
Li, J., Yan, K. and Ye, X.. Recurrence properties and disjointness on the induced spaces. Discrete Contin. Dyn. Syst. 35 (2015), 1059–1073.Google Scholar
Nadler, S.. Continuum Theory. An Introduction (Monographs and Textbooks in Pure and Applied Mathematics) . Marcel Dekker, New York, 1992.Google Scholar
Numakura, K.. On bicompact semigroups. Math. J. Okayama Univ. 1 (1952), 99–108.Google Scholar
Oprocha, P.. Weak mixing and product recurrence. Ann. Inst. Fourier (Grenoble) 60 (2010), 1233–1257.Google Scholar
Weiss, B.. Multiple recurrence and doubly minimal systems. Topological Dynamics and Applications (Minneapolis, MN, 1995) (Contemporary Mathematics, 215) . American Mathematical Society, Providence, RI, 1998, pp. 189–196.CrossRefGoogle Scholar
Ye, X. and Zhang, R.. On sensitive sets in topological dynamics. Nonlinearity 21 (2008), 1601–1620.Google Scholar