Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-10T21:34:49.653Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortices over Riemann surfaces and dominated splittings

Part of: Dynamical systems with hyperbolic behavior Riemann surfaces

Published online by Cambridge University Press:  02 February 2021

THOMAS METTLER Open the ORCID record for THOMAS METTLER [Opens in a new window]  and
GABRIEL P. PATERNAIN
THOMAS METTLER*
Affiliation:
Institut für Mathematik, Goethe-Universität Frankfurt, 60325Frankfurt am Main, Germany (e-mail: [email protected])
GABRIEL P. PATERNAIN
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, CambridgeCB3 0WB, UK (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We associate a flow 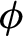$\phi $ with a solution of the vortex equations on a closed oriented Riemannian 2-manifold 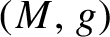$(M,g)$ of negative Euler characteristic and investigate its properties. We show that 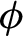$\phi $ always admits a dominated splitting and identify special cases in which 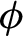$\phi $ is Anosov. In particular, starting from holomorphic differentials of fractional degree, we produce novel examples of Anosov flows on suitable roots of the unit tangent bundle of 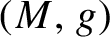$(M,g)$ .

Keywords

thermostatsvortex equationsAnosov flowsdominated splittingfractional differentials

MSC classification

Primary: 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.)
Secondary: 37D30: Partially hyperbolic systems and dominated splittings 30F30: Differentials on Riemann surfaces
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 5 , May 2022 , pp. 1781 - 1806
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arroyo, A. and Rodriguez Hertz, F.. Homoclinic bifurcations and uniform hyperbolicity for three-dimensional flows. Ann. Inst. H. Poincaré Anal. Non Linéaire 20 (2003), 805–841.Google Scholar
Asaoka, M.. Regular projectively Anosov flows on three-dimensional manifolds. Ann. Inst. Fourier (Grenoble) 60 (2010), 1649–1684.CrossRefGoogle Scholar
Benoist, Y.. Convexes divisibles. I. Algebraic Groups and Arithmetic. Tata Institute of Fundamental Research, Mumbai, 2004, pp. 339–374.Google Scholar
Bochi, J. and Gourmelon, N.. Some characterizations of domination. Math. Z. 263 (2009), 221–231.CrossRefGoogle Scholar
Bochi, J., Potrie, R. and Sambarino, A.. Anosov representations and dominated splittings. J. Eur. Math. Soc. (JEMS) 21 (2019), 3343–3414.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity, A Global Geometric and Probabilistic Perspective, Mathematical Physics, III (Encyclopaedia of Mathematical Sciences, 102). Springer, Berlin, 2005.Google Scholar
Bradlow, S. B.. Vortices in holomorphic line bundles over closed Kähler manifolds. Comm. Math. Phys. 135 (1990), 1–17.CrossRefGoogle Scholar
Bryant, R. L.. Projectively flat Finsler $2$ -spheres of constant curvature. Selecta Math. (N.S.) 3 (1997), 161–203.CrossRefGoogle Scholar
Cieliebak, K., Gaio, A. R., Mundet, I. Riera, I and Salamon, D. A.. The symplectic vortex equations and invariants of Hamiltonian group actions. J. Symplectic Geom. 1 (2002), 543–645.CrossRefGoogle Scholar
Crovisier, S. and Potrie, R.. Introduction to partially hyperbolic dynamics. School on Dynamical Systems. International Centre for Theoretical Physics, Trieste, 2015.Google Scholar
Dunajski, M.. Abelian vortices from sinh-Gordon and Tzitzeica equations. Phys. Lett. B 710 (2012), 236–239.CrossRefGoogle Scholar
Eliashberg, Y. M. and Thurston, W. P.. Confoliations (University Lecture Series, 13). American Mathematical Society, Providence, RI, 1998.Google Scholar
Gallavotti, G.. New methods in nonequilibrium gases and fluids, Open Syst. Inf. Dyn. 6 (1999), 101–136.CrossRefGoogle Scholar
Gallavotti, G. and Ruelle, D.. SRB states and nonequilibrium statistical mechanics close to equilibrium. Comm. Math. Phys. 190 (1997), 279–285.CrossRefGoogle Scholar
Geiges, H. and Gonzalo Pérez, J.. Generalised spin structures on 2-dimensional orbifolds. Osaka J. Math. 49 (2012), 449–470.Google Scholar
Ghys, E.. Flots d’Anosov sur les $3$ -variétés fibrées en cercles. Ergod. Th. & Dynam. Sys. 4 (1984), 67–80.CrossRefGoogle Scholar
Hitchin, N.. The self-duality equations on a Riemann surface. Proc. Lond. Math. Soc. (3) 55 (1987), 59–126.CrossRefGoogle Scholar
Hopf, E.. Closed surfaces without conjugate points. Proc. Natl. Acad. Sci. USA 34 (1948), 47–51.CrossRefGoogle ScholarPubMed
Jaffe, A. and Taubes, C.. Vortices and Monopoles, Structure of Static Gauge Theories (Progress in Physics, 2). Birkhäuser, Boston, MA, 1980.Google Scholar
Kim, I. and Papadopoulos, A.. Convex real projective structures and Hilbert metrics. Handbook of Hilbert Geometry (IRMA Lectures in Mathematics and Theoretical Physics, 22). European Mathematical Society, Zürich, 2014, pp. 307–338.Google Scholar
Labourie, F.. Anosov flows, surface groups and curves in projective space. Invent. Math. 165 (2006), 51–114.CrossRefGoogle Scholar
Labourie, F.. Flat projective structures on surfaces and cubic holomorphic differentials. Pure Appl. Math. Q. 3 (2007), 1057–1099.CrossRefGoogle Scholar
Loftin, J. C.. Affine spheres and convex ${\mathbb{RP}}^n$ -manifolds. Amer. J. Math. 123 (2001), 255–274.CrossRefGoogle Scholar
Mettler, T.. Minimal Lagrangian connections on compact surfaces. Adv. Math. 354 (2019), 106747, 36 p.CrossRefGoogle Scholar
Mettler, T. and Paternain, G. P.. Holomorphic differentials, thermostats and Anosov flows. Math. Ann. 373 (2019), 553–580.CrossRefGoogle Scholar
Mettler, T. and Paternain, G. P.. Convex projective surfaces with compatible Weyl connection are hyperbolic. Anal. PDE 13 (2020), 1073–1097.CrossRefGoogle Scholar
Mitsumatsu, Y.. Anosov flows and non-Stein symplectic manifolds. Ann. Inst. Fourier (Grenoble) 45 (1995), 1407–1421.CrossRefGoogle Scholar
Noguchi, M.. Yang–Mills–Higgs theory on a compact Riemann surface. J. Math. Phys. 28 (1987), 2343–2346.CrossRefGoogle Scholar
Ruelle, D.. Smooth dynamics and new theoretical ideas in nonequilibrium statistical mechanics. J. Statist. Phys. 95 (1999), 393–468.CrossRefGoogle Scholar
Sambarino, M.. A (short) survey on dominated splittings. Mathematical Congress of the Americas (Contemporary Mathematics, 656). American Mathematical Society, Providence, RI, 2016, pp. 149–183.CrossRefGoogle Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar
Taylor, M. E.. Partial Differential Equations III. Nonlinear Equations (Applied Mathematical Sciences, 117), 2nd edn. Springer, New York, NY, 2011.CrossRefGoogle Scholar
Wojtkowski, M. P.. Magnetic flows and Gaussian thermostats on manifolds of negative curvature. Fund. Math. 163 (2000), 177–191.CrossRefGoogle Scholar
Wojtkowski, M. P.. $W$ -flows on Weyl manifolds and Gaussian thermostats. J. Math. Pures Appl. (9) 79 (2000), 953–974.CrossRefGoogle Scholar
Wojtkowski, M. P.. Monotonicity, ${\mathcal{J}}$ -algebra of Potapov and Lyapunov exponents. Smooth Ergodic Theory and its Applications (Seattle, WA, 1999) (Proceedings of Symposia in Pure Mathematics, 69). American Mathematical Society, Providence, RI, 2001, pp. 499–521.CrossRefGoogle Scholar