Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Burton, Robert M.
and
Keller, Gerhard
1993.
Stationary measures for randomly chosen maps.
Journal of Theoretical Probability,
Vol. 6,
Issue. 1,
p.
1.
Quasf, Anthony N.
1996.
Non-ergodicity for C1 expanding maps and g-measures.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 3,
p.
531.
Stenflo, Örjan
2002.
Fractals in Multimedia.
Vol. 132,
Issue. ,
p.
13.
GALLO, SANDRO
and
TAKAHASHI, DANIEL Y.
2014.
Attractive regular stochastic chains: perfect simulation and phase transition.
Ergodic Theory and Dynamical Systems,
Vol. 34,
Issue. 5,
p.
1567.
C, Gallesco
S, Gallo
and
Y, Takahashi D
2014.
Explicit estimates in the Bramson–Kalikow model.
Nonlinearity,
Vol. 27,
Issue. 9,
p.
2281.
Friedli, Sacha
2015.
A note on the Bramson–Kalikow process.
Brazilian Journal of Probability and Statistics,
Vol. 29,
Issue. 2,
Hulse, Paul
2015.
Bernoulli Gibbs states for amenable group actions.
Dynamical Systems,
Vol. 30,
Issue. 2,
p.
137.
Dias, J. C. A.
and
Friedli, S.
2016.
Uniqueness vs. non-uniqueness for complete connections with modified majority rules.
Probability Theory and Related Fields,
Vol. 164,
Issue. 3-4,
p.
893.
Bethuelsen, Stein Andreas
and
Conache, Diana
2018.
One-Sided Continuity Properties for the Schonmann Projection.
Journal of Statistical Physics,
Vol. 172,
Issue. 4,
p.
1147.
Cioletti, L.
and
Lopes, A. O.
2019.
Correlation inequalities and monotonicity properties of the Ruelle operator.
Stochastics and Dynamics,
Vol. 19,
Issue. 06,
p.
1950048.
Ferreira, Ricardo F
Gallo, Sandro
and
Paccaut, Frédéric
2020.
Non-regular g-measures and variable length memory chains.
Nonlinearity,
Vol. 33,
Issue. 11,
p.
6026.


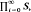 where
where 