Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
FISHMAN, LIOR
MANCE, BILL
SIMMONS, DAVID
and
URBAŃSKI, MARIUSZ
2015.
SHRINKING TARGETS FOR NONAUTONOMOUS DYNAMICAL SYSTEMS CORRESPONDING TO CANTOR SERIES EXPANSIONS.
Bulletin of the Australian Mathematical Society,
Vol. 92,
Issue. 2,
p.
205.
ZHANG, MENGJIE
2018.
HAUSDORFF DIMENSION OF THE EXCEPTIONAL SETS CONCERNING THE RUN-LENGTH FUNCTION OF BETA-EXPANSION.
Fractals,
Vol. 26,
Issue. 05,
p.
1850074.
Zheng, Lixuan
2019.
Diophantine approximation and run-length function on β-expansions.
Journal of Number Theory,
Vol. 202,
Issue. ,
p.
60.
Bugeaud, Yann
Liao, Lingmin
and
Rams, Michał
2019.
Metrical Results on the Distribution of Fractional Parts of Powers of Real Numbers.
Proceedings of the Edinburgh Mathematical Society,
Vol. 62,
Issue. 2,
p.
505.
Kim, Dong Han
and
Liao, Lingmin
2019.
Dirichlet Uniformly Well-approximated Numbers.
International Mathematics Research Notices,
Vol. 2019,
Issue. 24,
p.
7691.
ASPENBERG, MAGNUS
and
PERSSON, TOMAS
2019.
Shrinking targets in parametrised families.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 166,
Issue. 2,
p.
265.
Kirsebom, Maxim
Kunde, Philipp
and
Persson, Tomas
2020.
Shrinking targets and eventually always hitting points for interval maps.
Nonlinearity,
Vol. 33,
Issue. 2,
p.
892.
Zheng, Lixuan
and
Wu, Min
2020.
Uniform recurrence properties for beta-transformation.
Nonlinearity,
Vol. 33,
Issue. 9,
p.
4590.
Li, Y.-Q.
2020.
Digit frequencies of beta-expansions.
Acta Mathematica Hungarica,
Vol. 162,
Issue. 2,
p.
403.
Feng, Jing
and
Xu, Jian
2021.
Sets of Dirichlet non-improvable numbers with certain order in the theory of continued fractions
*
.
Nonlinearity,
Vol. 34,
Issue. 3,
p.
1598.
Ganotaki, Charis
and
Persson, Tomas
2021.
On eventually always hitting points.
Monatshefte für Mathematik,
Vol. 196,
Issue. 4,
p.
763.
HAN, YAN
and
MA, CHAO
2021.
UNIFORM DIOPHANTINE APPROXIMATION TO CANTOR SERIES EXPANSION.
Fractals,
Vol. 29,
Issue. 07,
Li, Yao-Qiang
2023.
Expansions of generalized Thue-Morse numbers.
Advances in Applied Mathematics,
Vol. 143,
Issue. ,
p.
102456.
Li, Yao-Qiang
2023.
Bifurcations of digit frequencies in unique expansions.
Journal of Number Theory,
Vol. 248,
Issue. ,
p.
420.
HE, YUBIN
and
LIAO, LINGMIN
2024.
Uniform approximation problems of expanding Markov maps.
Ergodic Theory and Dynamical Systems,
Vol. 44,
Issue. 1,
p.
159.
Jiang, Zhu
and
Xu, Jian
2024.
Hausdorff dimension of certain sets arising by the maximal run-length function over factorial language.
Journal of Mathematical Analysis and Applications,
Vol. 538,
Issue. 1,
p.
128325.
Wang, Bo
Li, Bing
and
Li, Ruofan
2024.
Uniform Diophantine approximation with restricted denominators.
Journal of Number Theory,
Vol. 260,
Issue. ,
p.
232.
WANG, BO
and
LI, BING
2024.
METRIC RESULTS FOR THE EVENTUALLY ALWAYS HITTING POINTS AND LEVEL SETS IN SUBSHIFT WITH SPECIFICATION.
Fractals,
Vol. 32,
Issue. 06,
TAN, BO
and
ZHOU, QING-LONG
2025.
Uniform Diophantine approximation and run-length function in continued fractions.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 4,
p.
1246.
Lü, Fan
Wang, Baowei
and
Wu, Jun
2025.
Diophantine approximation of the orbits of any given point under the family of beta-transformations.
Israel Journal of Mathematics,
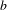 $b$-ary and
$b$-ary and  ${\it\beta}$-expansions
${\it\beta}$-expansions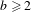 $b\geq 2$ be an integer and
$b\geq 2$ be an integer and 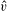 $\hat{v}$ a real number. Among other results, we compute the Hausdorff dimension of the set of real numbers
$\hat{v}$ a real number. Among other results, we compute the Hausdorff dimension of the set of real numbers 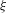 ${\it\xi}$ with the property that, for every sufficiently large integer
${\it\xi}$ with the property that, for every sufficiently large integer 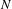 $N$, there exists an integer
$N$, there exists an integer  $n$ such that
$n$ such that 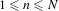 $1\leq n\leq N$ and the distance between
$1\leq n\leq N$ and the distance between 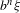 $b^{n}{\it\xi}$ and its nearest integer is at most equal to
$b^{n}{\it\xi}$ and its nearest integer is at most equal to 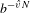 $b^{-\hat{v}N}$. We further solve the same question when replacing
$b^{-\hat{v}N}$. We further solve the same question when replacing 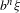 $b^{n}{\it\xi}$ by
$b^{n}{\it\xi}$ by 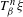 $T_{{\it\beta}}^{n}{\it\xi}$, where
$T_{{\it\beta}}^{n}{\it\xi}$, where 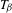 $T_{{\it\beta}}$ denotes the classical
$T_{{\it\beta}}$ denotes the classical 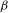 ${\it\beta}$-transformation.
${\it\beta}$-transformation.

