Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T04:48:36.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Thurston equivalence for rational maps with clusters

Published online by Cambridge University Press:  08 May 2012

THOMAS SHARLAND
THOMAS SHARLAND*
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate rational maps with period-one and period-two cluster cycles. Given the definition of a cluster, we show that, in the case where the degree is 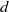$d$ and the cluster is fixed, the Thurston class of a rational map is fixed by the combinatorial rotation number 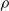$\rho $ and the critical displacement 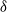$\delta $of the cluster cycle. The same result will also be proved in the case where the rational map is quadratic and has a period-two cluster cycle, and we will also show that the statement is no longer true in the higher-degree case.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 4 , August 2013 , pp. 1178 - 1198
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Douady, A. and Hubbard, J. H.. Étude dynamique des polynômes complexes, I. Publ. Math. d’Orsay 84-02, 1984.Google Scholar
[2]Douady, A. and Hubbard, J. H.. Étude dynamique des polynômes complexes, II. Publ. Math. d’Orsay 85-04, 1985.Google Scholar
[3]Douady, A. and Hubbard, J. H.. A proof of Thurston’s topological characterization of rational functions. Acta. Math. 171 (1993), 263–297.CrossRefGoogle Scholar
[4]Epstein, A. and Sharland, T.. A classification of bicritical rational maps with a pair of period two superattracting cycles. J. Lond. Math. Soc. (2) to appear.Google Scholar
[5]Fatou, P.. Sur les équations fonctionelles. Bull. Soc. Math. France 47 (1919), 161–271.CrossRefGoogle Scholar
[6]Fatou, P.. Sur les équations fonctionelles. Bull. Soc. Math. France 48 (1920), 33–94 and 208–314.Google Scholar
[7]Julia, G.. Memoire sur l’itération des fonctions rationelles. J. Math. Pure. Appl. 8 (1918), 47–245.Google Scholar
[8]Milnor, J.. On rational maps with two critical points. Experiment. Math. 9 (2000), 481–522.CrossRefGoogle Scholar
[9]Milnor, J.. Pasting together Julia sets: A worked out example of mating. Experiment. Math. 13 (2004), 55–92.CrossRefGoogle Scholar
[10]Rees, M.. Components of degree two hyperbolic rational maps. Invent. Math. 100(2) (1990).Google Scholar
[11]Rees, M.. A partial description of parameter space of rational maps of degree two: Part I. Acta Math. 168 (1992), 11–87.Google Scholar
[12]Rees, M.. Open problems submitted to the Workshop on Matings in Toulouse. Manuscript at http://www.liv.ac.uk/∼maryrees/papershomepage.html, 2011.Google Scholar
[13]Sharland, T.. Constructing rational maps with cluster points using the mating operation. J. Lond. Math. Soc. (2) to appear, arXiv:1108.5324v1.Google Scholar
[14]Sharland, T. J.. Rational maps with clustering and the mating of polynomials. PhD Thesis, University of Warwick, 2011. http://wrap.warwick.ac.uk/35776/.Google Scholar
[15]Shishikura, M. and Tan, L.. A family of cubic rational maps and matings of cubic polynomials. Experiment. Math. 9 (2000), 29–53.Google Scholar
[16]Tan, L.. Matings of quadratic polynomials. Ergod. Th. & Dynam. Sys. 12 (1992), 589–620.Google Scholar
[17]Youngs, J. W. T.. The extension of a homeomorphism defined on the boundary of a $2$-manifold. Bull. Amer. Math. Soc. 54(8) (1948), 805–808.Google Scholar