Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-08T13:24:39.043Z Has data issue: false hasContentIssue false
  • English
  • Français

Symbolic dynamics in mean dimension theory

Part of: Ergodic theory Smooth dynamical systems: general theory Communication, information Topological dynamics

Published online by Cambridge University Press:  15 June 2020

MAO SHINODA  and
MASAKI TSUKAMOTO
MAO SHINODA
Affiliation:
Department of Human Coexistence, Graduate School of Human and Environmental Studies, Kyoto University, Yoshida-Nihonmaths-cho, Sakyo-ku, Kyoto606-8501, Japan (e-mail: [email protected])
MASAKI TSUKAMOTO
Affiliation:
Department of Mathematics, Kyushu University, Moto-oka 744, Nishi-ku, Fukuoka819-0395, Japan (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Furstenberg [Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Syst. Theory1 (1967), 1–49] calculated the Hausdorff and Minkowski dimensions of one-sided subshifts in terms of topological entropy. We generalize this to 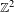$\mathbb{Z}^{2}$-subshifts. Our generalization involves mean dimension theory. We calculate the metric mean dimension and the mean Hausdorff dimension of 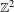$\mathbb{Z}^{2}$-subshifts with respect to a subaction of $\mathbb{Z}$. The resulting formula is quite analogous to Furstenberg’s theorem. We also calculate the rate distortion dimension of 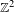$\mathbb{Z}^{2}$-subshifts in terms of Kolmogorov–Sinai entropy.

Keywords

subshiftmetric mean dimensionmean Hausdorff dimensionrate distortion dimension

MSC classification

Primary: 37B10: Symbolic dynamics 37C45: Dimension theory of dynamical systems
Secondary: 37A05: Measure-preserving transformations 94A34: Rate-distortion theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 8 , August 2021 , pp. 2542 - 2560
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cover, T. M. and Thomas, J. A.. Elements of Information Theory, 2nd edn. Wiley, New York, 2006.Google Scholar
Effros, M., Chou, P. A. and Gray, G. M.. Variable-rate source coding theorems for stationary nonergodic sources. IEEE Trans. Inform. Theory 40 (1994), 1920–1925.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 259). Springer, London, 2011.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.Google Scholar
Gutman, Y., Lindenstrauss, E. and Tsukamoto, M.. Mean dimension of ℤ k -actions. Geom. Funct. Anal. 26(3) (2016), 778–817.Google Scholar
Gray, R. M.. Entropy and Information Theory. Springer, New York, 1990.Google Scholar
Gromov, M.. Topological invariants of dynamical systems and spaces of holomorphic maps: I. Math. Phys. Anal. Geom. 2 (1999), 323–415.Google Scholar
Gutman, Y.. Mean dimension and Jaworski-type theorems. Proc. Lond. Math. Soc. (3) 111(4) (2015), 831–850.Google Scholar
Gutman, Y., Qiao, Y. and Tsukamoto, M.. Application of signal analysis to the embedding problem of ℤ k -actions. Geom. Funct. Anal. 29 (2019), 1440–1502.Google Scholar
Gutman, Y. and Tsukamoto, M.. Embedding minimal dynamical systems into Hilbert cubes. Invent. Math. 221 (2020), 113–166.Google Scholar
Kawabata, T. and Dembo, A.. The rate distortion dimension of sets and measures. IEEE Trans. Inform. Theory 40(5) (1994), 1564–1572.Google Scholar
Leon-Garcia, A., Davisson, L. D. and Neuhoff, D. L.. New results on coding of stationary nonergodic sources. IEEE Trans. Inform. Theory 25 (1979), 137–144.Google Scholar
Lindenstrauss, E.. Pointwise theorems for amenable groups. Invent. Math. 146 (2001), 259–296.Google Scholar
Lindenstrauss, E.. Mean dimension, small entropy factors and an embedding theorem. Publ. Math. Inst. Hautes Études Sci. 89 (1999), 227–262.Google Scholar
Li, H. and Liang, B.. Mean dimension, mean rank and von Neumann–Lück rank. J. Reine Angew. Math. 739 (2018), 207–240.Google Scholar
Lindenstrauss, E. and Tsukamoto, M.. From rate distortion theory to metric mean dimension: variational principle. IEEE Trans. Inform. Theory 64(5) (2018), 3590–3609.Google Scholar
Lindenstrauss, E. and Tsukamoto, M.. Double variational principle for mean dimension. Geom. Funct. Anal. 29 (2019), 1048–1109.Google Scholar
Lindenstrauss, E. and Weiss, B.. Mean topological dimension. Israel J. Math. 115 (2000), 1–24.Google Scholar
Mañé, R.. Expansive homeomorphisms and topological dimension. Trans. Amer. Math. Soc. 252 (1979), 313–319.Google Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces, Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics, 44). Cambridge University Press, Cambridge, 1995.Google Scholar
Meyerovitch, T. and Tsukamoto, M.. Expansive multiparameter actions and mean dimension. Trans. Amer. Math. Soc. 371 (2019), 7275–7299.Google Scholar
Ornstein, D. S. and Weiss, B.. The Shannon–McMillan–Breiman theorem for a class of amenable groups. Israel J. Math. 44 (1983), 53–60.Google Scholar
Rényi, A.. On the dimension and entropy of probability distributions. Acta Math. Acad. Sci. Hungar. 10 (1959), 193–215.Google Scholar
Rudolph, D. J.. Fundamentals of Measurable Dynamics. Clarendon Press, Oxford, 1990.Google Scholar
Shannon, C. E.. A mathematical theory of communication. Bell Syst. Tech. J. 27 (1948), 379–423, 623–656.Google Scholar
Shannon, C. E.. Coding theorems for a discrete source with a fidelity criterion. IRE National Convention Record 7(4) (1959), 142–163.Google Scholar
Tsukamoto, M.. Mean dimension of the dynamical system of Brody curves. Invent. Math. 211 (2018), 935–968.Google Scholar
Young, L.-S.. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2 (1982), 109–124.Google Scholar