Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T01:55:41.287Z Has data issue: false hasContentIssue false
  • English
  • Français

A symbolic characterization of the horseshoe locus in the Hénon family

Published online by Cambridge University Press:  08 March 2016

ERIC BEDFORD  and
JOHN SMILLIE
ERIC BEDFORD
Affiliation:
Mathematics Department, Stony Brook University, Stony Brook, NY 11794-3651, USA email [email protected]
JOHN SMILLIE
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the family of quadratic Hénon diffeomorphisms of the plane 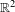$\mathbb{R}^{2}$. A map will be said to be a ‘horseshoe’ if its restriction to the non-wandering set is hyperbolic and conjugate to the full 2-shift. We give a criterion for being a horseshoe based on an auxiliary coding which describes positions of points relative to the stable manifold of one of the fixed points. In addition we describe the topological conjugacy type of maps on the boundary of the horseshoe locus. We use complex techniques and we work with maps in a parameter region which is a two-dimensional analog of the familiar ‘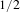$1/2$-wake’ for the quadratic family 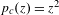$p_{c}(z)=z^{2}$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 5 , August 2017 , pp. 1389 - 1412
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arai, Z. and Ishii, Y.. On parameter loci of the Hénon family. Preprint, 2015, arXiv:1501.01368.Google Scholar
Bedford, E., Lyubich, M. and Smillie, J.. Polynomial diffeomorphisms of C 2 . IV: the measure of maximal entropy and laminar currents. Invent. Math. 112 (1993), 77–125.CrossRefGoogle Scholar
Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of C 2 . VII: hyperbolicity and external rays. Ann. Sci. Éc. Norm. Supér. (4) 32(4) (1999), 455–497.CrossRefGoogle Scholar
Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of C 2 . VIII: quasi-expansion. Amer. J. Math. 124 (2002), 221–271.CrossRefGoogle Scholar
Bedford, E. and Smillie, J.. The Hénon family: the complex horsehoe locus and real parameter space. Complex Dynamics (Contemporary Mathematics, 396) . American Mathematical Society, Providence, RI, 2006, pp. 21–36.Google Scholar
Bedford, E. and Smillie, J.. Real polynomial diffeomorphisms with maximal entropy: tangencies. Ann. of Math. (2) 160 (2004), 1–25.CrossRefGoogle Scholar
Bedford, E. and Smillie, J.. Real polynomial diffeomorphisms with maximal entropy. II. Small Jacobian. Ergod. Th. & Dynam. Syst. 26(5) (2006), 1259–1283.CrossRefGoogle Scholar
Cvitanović, P.. Periodic orbits as the skeleton of classical and quantum chaos. Nonlinear Science: The Next Decade (Los Alamos, NM, 1990). Phys. D 51(1) (1991), 138–151.Google Scholar
Cao, Y., Luzzatto, S. and Rios, I.. Some non-hyperbolic systems with strictly non-zero Lyapunov exponents for all invariant measures: horseshoes with internal tangencies. Discrete Contin. Dyn. Syst. 15 (2006), 61–71.Google Scholar
Cao, Y., Luzzatto, S. and Rios, I.. The boundary of hyperbolicity for Hénon-like families. Ergod. Th. & Dynam. Syst. 28(4) (2008), 1049–1080.Google Scholar
Carleson, L., Jones, P. and Yoccoz, J.-C.. Julia and John. Bol. Soc. Brasil. Mat. (N.S.) 25(1) (1994), 1–30.Google Scholar
De Carvalho, A. and Hall, T.. How to prune a horseshoe. Nonlinearity 15 (2002), R19–R68.CrossRefGoogle Scholar
Dinh, T.-C., Dujardin, R. and Sibony, N.. On the dynamics near infinity of some polynomial mappings in C 2 . Math. Ann. 333(4) (2005), 703–739.Google Scholar
Dujardin, R.. Hénon-like mappings in C 2 . Amer. J. Math. 126(2) (2004), 439–472.CrossRefGoogle Scholar
Hubbard, J. H. and Oberste-Vorth, R.. Hénon mappings in the complex domain. II: projective and inductive limits of polynomials. Real and Complex Dynamical Systems (Hillerød, 1993) (Nato Science Series C, 464) . Kluwer Academic Publishers, Dordrecht, 1995, pp. 89–132.CrossRefGoogle Scholar
Hagiwara, R. and Shudo, A.. An algorithm to prune the area-preserving Hénon map. J. Phys. A 37(44) (2004), 10521–10543.Google Scholar
Hoensch, U.. Horseshoe-type diffeomorphisms with a homoclinic tangency at the boundary of hyperbolicity. PhD Thesis, Michigan State University, 2003, 57pp.Google Scholar
Hoensch, U.. Some hyperbolicity results for Hénon-like diffeomorphisms. Nonlinearity 21(3) (2008), 587–611.Google Scholar
Ishii, Y.. Hyperbolic polynomial diffeomorphisms of C 2 . I: a non-planar map. Adv. Math. 218(2) (2008), 417–464.CrossRefGoogle Scholar
Ishii, Y. and Smillie, J.. Homotopy shadowing. Amer. J. Math. 132(4) (2010), 987–1029.CrossRefGoogle Scholar
Lipa, C.. Monodromy and Hénon mappings. PhD Thesis, Cornell University, 2009.Google Scholar
Milnor, J.. Periodic orbits, external rays and the Mandelbrot set: an expository account. Géométrie Complexe et systèmes Dynamiques (Orsay, 1995). Astérisque 261 (2000), xiii, 277–333.Google Scholar
Takahasi, H.. Prevalence of non-uniform hyperbolicity at the first bifurcation of Hénon-like families. Preprint, 2013, arXiv:1308.4199 [math.DS].Google Scholar
Willard, S.. General Topology. Addison-Wesley, Reading, MA, 1970.Google Scholar