No CrossRef data available.
Article contents
Sur le spectre des opérateurs rigides
Published online by Cambridge University Press: 01 March 2022
Abstract
For any
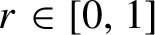 $r\in [0,1]$
we give an example of a rigid operator whose spectrum is the annulus
$r\in [0,1]$
we give an example of a rigid operator whose spectrum is the annulus
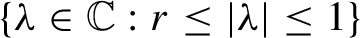 $\{\lambda\in \mathbb{C} : r \le |\lambda| \le 1 \} $
. In particular, when
$\{\lambda\in \mathbb{C} : r \le |\lambda| \le 1 \} $
. In particular, when
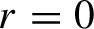 $r=0$
this operator is rigid and non-invertible, and when
$r=0$
this operator is rigid and non-invertible, and when
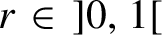 $r\in {\kern1pt}] 0,1 [ $
this operator is invertible but its inverse is not rigid. This answers two questions of Costakis, Manoussos and Parissis [Recurrent linear operators. Complex Anal. Oper. Theory 8 (2014), 1601–1643].
$r\in {\kern1pt}] 0,1 [ $
this operator is invertible but its inverse is not rigid. This answers two questions of Costakis, Manoussos and Parissis [Recurrent linear operators. Complex Anal. Oper. Theory 8 (2014), 1601–1643].
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
Pour Mustapha Krazem, à l’occasion de son soixantiéme anniversaire



