Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T14:37:21.137Z Has data issue: false hasContentIssue false
  • English
  • Français

A spectral strong approximation theorem for measure-preserving actions

Part of: Ergodic theory

Published online by Cambridge University Press:  06 September 2018

MIKLÓS ABÉRT
MIKLÓS ABÉRT*
Affiliation:
MTA Renyi Institute of Mathematics, Realtanoda utca 13–15, Budapest 1053, Hungary email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\unicode[STIX]{x1D6E4}$ be a finitely generated group acting by probability measure-preserving maps on the standard Borel space 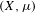$(X,\unicode[STIX]{x1D707})$. We show that if 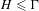$H\leq \unicode[STIX]{x1D6E4}$ is a subgroup with relative spectral radius greater than the global spectral radius of the action, then 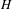$H$ acts with finitely many ergodic components and spectral gap on 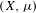$(X,\unicode[STIX]{x1D707})$. This answers a question of Shalom who proved this for normal subgroups.

Keywords

group actions

MSC classification

Primary: 37A30: Ergodic theorems, spectral theory, Markov operators
Secondary: 37A15: General groups of measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 4 , April 2020 , pp. 865 - 880
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abert, M. and Elek, G.. Dynamical properties of profinite actions. Ergod. Th. & Dynam. Sys. 32(6) (2012), 1805–1835.Google Scholar
Abert, M. and Nikolov, N.. Rank gradient, cost of groups and the rank vs Heegaard genus conjecture. J. Eur. Math. Soc. 14(5) (2012), 1657–1677.Google Scholar
Abert, M., Glasner, Y. and Virag, B.. Kesten’s theorem for invariant random subgroups. Duke Math. J. 163(3) (2014), 465–488.Google Scholar
Backhausz, A., Szegedy, B. and Virag, B.. Ramanujan graphings and correlation decay in local algorithms. Random Struct. Algor. 47(3) (2015), 424–435.Google Scholar
Bader, U., Duchesne, B. and Lecureux, J.. Amenable invariant random subgroups. Israel J. Math. 213(1) (2016), 399–422.Google Scholar
Bourgain, J. and Gamburd, A.. Uniform expansion bounds for Cayley graphs of SL 2(𝔽p). Ann. of Math. (2) 167(2) (2008), 625–642.Google Scholar
Bourgain, A. and Varjú, P.. Expansion in SL d(ℤ/qℤ), q arbitrary. Invent. Math. 188(1) (2012), 151–173.Google Scholar
Breuillard, E., Green, B. and Tao, T.. Approximate subgroups of linear groups. Geom. Funct. Anal. 21(4) (2011), 774–819.Google Scholar
Gamburd, A.. On the spectral gap for infinite index ‘congruence’ subgroups of SL 2(ℤ). Israel J. Math. 127 (2002), 157–200.Google Scholar
Glasner, Y.. Strong approximation in random towers of graphs. Combinatorica 34(2) (2014), 139–171.Google Scholar
Golsefidy, A. S. and Varjú, P.. Expansion in perfect groups. Geom. Funct. Anal. 22(6) (2012), 1832–1891.Google Scholar
Helfgott, H. A.. Growth and generation in SL 2(ℤ/pℤ). Ann. of Math. (2) 167(2) (2008), 601–623.Google Scholar
Kechris, A. S. and Tsankov, T.. Amenable actions and almost invariant sets. Proc. Amer. Math. Soc. 136(2) (2008), 687–697.Google Scholar
Kesten, H.. Symmetric random walks on groups. Trans. Amer. Math. Soc. 92 (1959), 336–354.Google Scholar
Lindenstrauss, E. and Varju, P. P.. Random walks in the group of Euclidean isometries and self-similar measures. Duke Math. J. 165(6) (2016), 1061–1127.Google Scholar
Lyons, R. and Nazarov, F.. Perfect matchings as IID factors on non-amenable groups. Eur. J. Combin. 32(7) (2011), 1115–1125.Google Scholar
Lubotzky, A., Phillips, R. and Sarnak, P.. Ramanujan graphs. Combinatorica 8(3) (1988), 261–277.Google Scholar
Pyber, L. and Szabó, E.. Growth in finite simple groups of Lie type of bounded rank. J. Amer. Math. Soc. 29 (2016), 95–146.Google Scholar
Schmidt, K.. Amenability, Kazhdan’s property T, strong ergodicity and invariant means for ergodic group-actions. Ergod. Th. & Dynam. Sys. 1(2) (1981), 223–236.Google Scholar
Shalom, Y.. Expanding graphs and invariant means. Combinatorica 17(4) (1997), 555–575.Google Scholar