Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T03:07:50.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral gap property and strong ergodicity for groups of affine transformations of solenoids

Part of: Noncompact transformation groups Ergodic theory

Published online by Cambridge University Press:  11 October 2018

BACHIR BEKKA  and
CAMILLE FRANCINI
BACHIR BEKKA
Affiliation:
Université de Rennes, CNRS, IRMAR-UMR 6625 Campus Beaulieu, F-35042 Rennes Cedex, France email [email protected], [email protected]
CAMILLE FRANCINI
Affiliation:
Université de Rennes, CNRS, IRMAR-UMR 6625 Campus Beaulieu, F-35042 Rennes Cedex, France email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $X$ be a solenoid, i.e. a compact, finite-dimensional, connected abelian group with normalized Haar measure $\unicode[STIX]{x1D707}$, and let 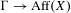$\unicode[STIX]{x1D6E4}\rightarrow \operatorname{Aff}(X)$ be an action of a countable discrete group 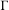$\unicode[STIX]{x1D6E4}$ by continuous affine transformations of 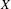$X$. We show that the probability measure preserving action 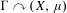$\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ does not have the spectral gap property if and only if there exists a 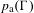$p_{\text{a}}(\unicode[STIX]{x1D6E4})$-invariant proper subsolenoid $Y$ of 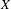$X$ such that the image of 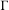$\unicode[STIX]{x1D6E4}$ in $\operatorname{Aff}(X/Y)$ is a virtually solvable group, where 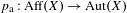$p_{\text{a}}:\operatorname{Aff}(X)\rightarrow \operatorname{Aut}(X)$ is the canonical projection. When 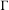$\unicode[STIX]{x1D6E4}$ is finitely generated or when 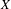$X$ is the $a$-adic solenoid for an integer 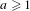$a\geq 1$, the subsolenoid $Y$ can be chosen so that the image $\unicode[STIX]{x1D6E4}$ in 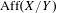$\operatorname{Aff}(X/Y)$ is a virtually abelian group. In particular, an action $\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ by affine transformations on a solenoid $X$ has the spectral gap property if and only if 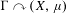$\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ is strongly ergodic.

Keywords

group actionsarithmetic algebraic dynamicsspectral gap propertystrong ergodicitysolenoids

MSC classification

Primary: 37A30: Ergodic theorems, spectral theory, Markov operators
Secondary: 22F10: Measurable group actions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 5 , May 2020 , pp. 1180 - 1193
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abért, M. and Elek, G.. Dynamical properties of profinite actions. Ergod. Th. & Dynam. Sys. 32 (2012), 1805–1835.Google Scholar
Bekka, B. and Guivarc’h, Y.. On the spectral theory of groups of affine transformations of compact nilmanifolds. Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), 607–645.Google Scholar
Bekka, B., de la Harpe, P. and Valette, A.. Kazhdan’s Property (T). Cambridge University Press, Cambridge, 2008.Google Scholar
Bekka, B.. Spectral rigidity of group actions on homogeneous spaces. Handbook of Group Actions, Volume III. Eds. Ji, L., Papadopoulos, A. and Yau, S.-T.. Preprint, 2016, to appear, arXiv:1602.02892.Google Scholar
Bourgain, J. and Gamburd, A.. A spectral gap theorem in SU(d). J. Eur. Math. Soc. (JEMS) 14 (2012), 1455–1511.Google Scholar
de Cornulier, Y.. Invariant probabilities on projective spaces. Unpublished notes 2004; available at:http://www.normalesup.org/∼cornulier/invmean.pdf.Google Scholar
Furstenberg, H.. A note on Borel’s density theorem. Proc. Amer. Math. Soc. 55 (1976), 209–212.Google Scholar
Furman, A. and Shalom, Y.. Sharp ergodic theorems for group actions and strong ergodicity. Ergod. Th. & Dynam. Sys. 19 (1999), 1037–1061.Google Scholar
Halmos, R.. On automorphisms of compact groups. Bull. Amer. Math. Soc. (N.S.) 49 (1943), 619–624.Google Scholar
Hewitt, E. and Ross, K.. Abstract Harmonic Analysis, Volume I (Die Grundlehren der Mathematischen Wissenschaften, 115). Springer, New York, 1963.Google Scholar
Humphreys, J.. Linear Algebraic Groups (Graduate Texts in Mathematics, 21). Springer, New York, 1975.Google Scholar
del Junco, A. and Rosenblatt, J.. Counterexamples in ergodic theory. Math. Ann. 245 (1979), 185–197.Google Scholar
Kaplansky, I.. Groups with representations of bounded degree. Canad. J. Math. 1 (1949), 105–112.Google Scholar
Kitchens, B. and Schmidt, K.. Automorphisms of compact groups. Ergod. Th. & Dynam. Sys. 9 (1989), 691–735.Google Scholar
Robert, A.. A Course in p-adic Analysis (Graduate Texts in Mathematics, 198). Springer, New York, 2000.Google Scholar
Schmidt, K.. Amenability, Kazhdan’s property T, strong ergodicity and invariant means for ergodic group-actions. Ergod. Th. & Dynam. Sys. 1 (1981), 223–236.Google Scholar
Tits, J.. Free subgroups in linear groups. J. Algebra 20 (1972), 250–270.Google Scholar
Weil, A.. Basic Number Theory (Die Grundlehren der Mathematischen Wissenschaften, 144). Springer, New York, 1967.Google Scholar