Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T04:28:33.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Some consequences of the shadowing property in low dimensions

Published online by Cambridge University Press:  08 March 2013

ANDRES KOROPECKI  and
ENRIQUE R. PUJALS
ANDRES KOROPECKI
Affiliation:
Universidade Federal Fluminense, Instituto de Matemática, Rua Mário Santos Braga S/N, 24020-140 Niteroi, RJ, Brazil email [email protected]
ENRIQUE R. PUJALS
Affiliation:
IMPA, Estrada Dona Castorina 110, 22460-320 Rio de Janeiro, RJ, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider low-dimensional systems with the shadowing property and we study the problem of existence of periodic orbits. In dimension two, we show that the shadowing property for a homeomorphism implies the existence of periodic orbits in every $\epsilon $-transitive class, and in contrast we provide an example of a 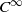${C}^{\infty } $ Kupka–Smale diffeomorphism with the shadowing property exhibiting an aperiodic transitive class. Finally, we consider the case of transitive endomorphisms of the circle, and we prove that the $\alpha $-Hölder shadowing property with 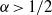$\alpha \gt 1/ 2$ implies that the system is conjugate to an expanding map.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1273 - 1309
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlfors, L. V. and Sario, L.. Riemann Surfaces (Princeton Mathematical Series, 26). Princeton University Press, Princeton, NJ, 1960.Google Scholar
Epstein, D. B. A.. Curves on 2-manifolds and isotopies. Acta Math. 115 (1966), 83–107.Google Scholar
Franks, J. and Misiurewicz, M.. Topological methods in dynamics. Handbook of Dynamical Systems, Vol. 1A. North-Holland, Amsterdam, 2002, pp. 547–598.Google Scholar
Franks, J.. Realizing rotation vectors for torus homeomorphisms. Trans. Amer. Math. Soc. 311 (1) (1989), 107–115.Google Scholar
Franks, J.. A new proof of the Brouwer plane translation theorem. Ergod. Th. & Dynam. Syst. 12 (2) (1992), 217–226.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
Kozlovski, O., Shen, W. and van Strien, S.. Density of hyperbolicity in dimension one. Ann. of Math. (2) 166 (1) (2007), 145–182.Google Scholar
Mañé, R.. Hyperbolicity, sinks and measure in one-dimensional dynamics. Comm. Math. Phys. 100 (4) (1985), 495–524.CrossRefGoogle Scholar
Mai, J. and Ye, X.. The structure of pointwise recurrent maps having the pseudo orbit tracing property. Nagoya Math. J. 166 (2002), 83–92.Google Scholar
Nitecki, Z.. On semi-stability for diffeomorphisms. Invent. Math. 14 (1971), 83–122.Google Scholar
Newhouse, S. and Palis, J.. Cycles and bifurcation theory. Astérisque 31 (1976), 43–140.Google Scholar
Pilyugin, S. Y.. Shadowing in Dynamical Systems (Lecture Notes in Mathematics, 1706). Springer, Berlin, 1999.Google Scholar
Pujals, E. R. and Sambarino, M.. On the dynamics of dominated splitting. Ann. of Math. (2) 169 (3) (2009), 675–739.Google Scholar
Pilyugin, S. Y. and Tikhomirov, S. B.. Lipschitz shadowing implies structural stability. Nonlinearity 23 (10) (2010), 2509–2515.Google Scholar
Richards, I.. On the classification of noncompact surfaces. Trans. Amer. Math. Soc. 106 (1963), 259–269.Google Scholar
Tikhomirov, S. B.. Holder shadowing on finite intervals. Preprint, arXiv:1106.4053, 2011.Google Scholar
Walters, P.. On the pseudo-orbit tracing property and its relationship to stability. The Structure of Attractors in Dynamical Systems (Proc. Conf., North Dakota State Univ., Fargo, N.D., 1977) (Lecture Notes in Mathematics, 668). Springer, Berlin, 1978, pp. 231–244.Google Scholar