Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T21:34:50.507Z Has data issue: false hasContentIssue false
  • English
  • Français

The singularity spectrum of the fish’s boundary

Published online by Cambridge University Press:  01 February 2008

JULIEN BRÉMONT  and
STÉPHANE SEURET
JULIEN BRÉMONT
Affiliation:
Laboratoire d’Analyse et de Mathématiques Appliquées, Université Paris XII, Faculté des Sciences et Technologies, 61 Avenue du Général de Gaulle, 94010 Créteil Cedex, France (email: [email protected], [email protected])
STÉPHANE SEURET
Affiliation:
Laboratoire d’Analyse et de Mathématiques Appliquées, Université Paris XII, Faculté des Sciences et Technologies, 61 Avenue du Général de Gaulle, 94010 Créteil Cedex, France (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 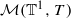be the convex set of Borel probability measures on the circle 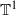invariant under the action of the transformation 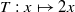(mod 1). Its projection on the complex plane by the application 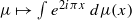is a compact convex subset of the unit disc, symmetric with respect to the x-axis, called the ‘fish’ by Bousch. Seeing the boundary of the upper half-fish as a function, we focus on its local regularity. We show that its multifractal spectrum is concentrated at 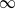, but that every pointwise regularity 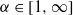is realized in an uncountable dense set of points. The results rely on fine properties of Sturm measures.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 1 , February 2008 , pp. 49 - 66
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Barral, J. and Seuret, S.. The singularity spectrum of Lévy processes in multifractal time. Adv. Math. 14(1) (2007), 437–468.CrossRefGoogle Scholar
[2]Brown, G., Michon, G. and Peyrière, J.. On the multifractal analysis of measures. J. Statist. Phys. 66(3–4) (1992), 775–790.CrossRefGoogle Scholar
[3]Bousch, T.. Le poisson n’a pas d’arêtes. Ann. Inst. H. Poincaré Probab. Statist. 36(4) (2000), 489–508.CrossRefGoogle Scholar
[4]Bousch, T. and Mairesse, J.. Asymptotic height optimization for topical IFS, Tetris heaps, and the finiteness conjecture. J. Amer. Math. Soc. 15(1) (2002), 77–111 (electronic).CrossRefGoogle Scholar
[5]Brémont, J.. Dynamics of injective quasi-contractions. Ergod. Th. & Dynam. Sys. 26 (2006), 19–44.CrossRefGoogle Scholar
[6]Brémont, J.. Finite flowers and maximizing measures for generic Lipschitz functions on the circle. Nonlinearity 19 (2006), 813–828.CrossRefGoogle Scholar
[7]Brémont, J.. Marches aléatoires en milieu aléatoire sur ; dynamique d’applications localement contractantes sur le cercle. Thèse de Doctorat, Université de Rennes I, 2002.Google Scholar
[8]Bugeaud, Y. and Conze, J.-P.. Dynamics of some contracting linear functions modulo 1. Noise, Oscillators and Algebraic Randomness (Chapelle des Bois, 1999). Springer, Berlin, 2000, pp. 379–387.CrossRefGoogle Scholar
[9]Bullett, S. and Sentenac, P.. Ordered orbits of the shift, square roots and the devil’s staircase. Math. Proc. Cambridge Philos. Soc. 115(3) (1994), 451–481.CrossRefGoogle Scholar
[10]Conze, J.-P. and Guivarc’h, Y.. Croissance des sommes ergodiques et principe variationnel. Technical Report Université de Rennes 1, 1990.Google Scholar
[11]Falconer, K.. Fractal Geometry, Mathematical Foundations and Applications. Wiley, Chichester, 1990.Google Scholar
[12]Frisch, U. and Parisi, G.. Fully developed turbulence and intermittency. Proc. Int. Summer School of Physics, Enrico Fermi. North Holland, Amsterdam, 1985, pp. 84–88.Google Scholar
[13]Gambaudo, J.-M. and Tresser, C.. On the dynamics of quasi-contractions. Bol. Soc. Brasil Mat. 19(1) (1988), 61–114.CrossRefGoogle Scholar
[14]Halsey, T., Jensen, M., Kadanoff, L., Procaccia, I. and Schraiman, B.. Fractal measures and their singularities: the characterization of strange sets. Phys. Rev. A 33(2) (1986), 1141–1151.CrossRefGoogle ScholarPubMed
[15]Hunt, B. and Ott, E.. Optimal periodic orbits of chaotic systems. Phys. Rev. Lett. 76 (1996), 2254–2257.CrossRefGoogle ScholarPubMed
[16]Jaffard, S.. The multifractal nature of Lévy processes. Probab. Theory Related Fields 114(2) (1999), 207–227.CrossRefGoogle Scholar
[17]Jaffard, S.. Multifractal functions: recent advances and open problems. Bull. Soc. Roy. Sci. Liège 73(2–3) (2004), 129–153.Google Scholar
[18]Jenkinson, O.. Frequency locking on the boundary of the barycenter set. Experiment. Math. 9(2) (2000), 309–317.CrossRefGoogle Scholar
[19]Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. 15(1) (2006), 197–224.CrossRefGoogle Scholar
[20]Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[21]Morse, M. and Hedlund, G. A.. Symbolic dynamics Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.CrossRefGoogle Scholar
[22]Pesin, Y. and Weiss, H.. The multifractal analysis of Gibbs measures: motivation, mathematical foundation and examples. Chaos 7(1) (1997), 89–106.CrossRefGoogle ScholarPubMed