Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T04:35:23.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Second-order ergodic theorem for self-similar tiling systems

Published online by Cambridge University Press:  04 July 2013

KONSTANTIN MEDYNETS  and
BORIS SOLOMYAK
KONSTANTIN MEDYNETS
Affiliation:
Department of Mathematics, US Naval Academy, Annapolis, MA 21402, USA email [email protected]
BORIS SOLOMYAK
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195-4350, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider infinite measure-preserving non-primitive self-similar tiling systems in Euclidean space 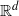${ \mathbb{R} }^{d} $. We establish the second-order ergodic theorem for such systems, with exponent equal to the Hausdorff dimension of a graph-directed self-similar set associated with the substitution rule.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 6 , December 2014 , pp. 2018 - 2053
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50). American Mathematical Society, Providence, RI, 1997.Google Scholar
Aaronson, J., Denker, M. and Fisher, A.. Second order ergodic theorems for ergodic transformations of infinite measure spaces. Proc. Amer. Math. Soc. 114 (1) (1992), 115–127.Google Scholar
Anderson, J. and Putnam, I.. Topological invariants for substitution tilings and their associated ${C}^{\ast } $-algebras. Ergod. Th. & Dynam. Sys. 18 (3) (1998), 509–537.Google Scholar
Becker, M.. A ratio ergodic theorem for groups of measure-preserving transformations. Illinois J. Math. 27 (1983), 562–570.Google Scholar
Bedford, T. and Fisher, A.. Analogues of the Lebesgue density theorem for fractal sets of reals and integers. Proc. Lond. Math. Soc. (3) 64 (1992), 95–124.Google Scholar
Bell, J.. Logarithmic frequency in morphic sequences. J. Théor. Nombres Bordeaux 20 (2) (2008), 227–241.CrossRefGoogle Scholar
Bezuglyi, S., Kwiatkowski, J. and Medynets, K.. Aperiodic substitution systems and their Bratteli diagrams. Ergod. Th. & Dynam. Sys. 29 (1) (2009), 37–72.CrossRefGoogle Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Invariant measures on stationary Bratteli diagrams. Ergod. Th. & Dynam. Sys. 30 (4) (2010), 973–1007.CrossRefGoogle Scholar
Cortez, M. I. and Solomyak, B.. Invariant measures for non-primitive tiling substitutions. J. Anal. Math. 115 (2011), 293–342.CrossRefGoogle Scholar
Danzer, L.. Inflation species of planar tilings which are not of locally finite complexity. Proc. Steklov Inst. Math. 239 (2002), 108–116.Google Scholar
Edgar, G.. Integral, Probability, and Fractal Measures. Springer, New York, 1997.Google Scholar
Falconer, K.. Techniques in Fractal Geometry. John Wiley & Sons, Chichester, 1997.Google Scholar
Fisher, A.. Integer Cantor sets and an order-two ergodic theorem. Ergod. Th. & Dynam. Sys. 13 (1) (1993), 45–64.CrossRefGoogle Scholar
Frank, N. P. and Robinson, E. A. Jr. Generalized $\beta $-expansions, substitution tilings, and local finiteness. Trans. Amer. Math. Soc. 360 (2008), 1163–1177.Google Scholar
Gantmacher, F. R.. Applications of the Theory of Matrices. Interscience, New York, 1959.Google Scholar
Hama, M. and Yuasa, H.. Invariant measures for subshifts arising from substitutions of some primitive components. Hokkaido Math. J. 40 (2) (2011), 279–312.CrossRefGoogle Scholar
Hochman, M.. A ratio ergodic theorem for multiparameter non-singular actions. J. Eur. Math. Soc. 12 (2) (2010), 365–383.Google Scholar
Hurewicz, W. and Wallman, H.. Dimension Theory (Princeton Mathematical Series, 4). Princeton University Press, Princeton, NJ, 1941.Google Scholar
Kenyon, R.. Self-Replicating Tilings. Symbolic Dynamics and its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135). American Mathematical Society, Providence, RI, 1992, pp. 239–263.Google Scholar
Kenyon, R.. The construction of self-similar tilings. Geom. Funct. Anal. 6 (3) (1996), 471–488.Google Scholar
Ledrappier, F. and Sarig, O.. Fluctuations of ergodic sums for horocycle flows on ${ \mathbb{Z} }^{d} $-covers of finite volume surfaces. Discrete Contin. Dyn. Syst. 22 (1–2) (2008), 247–325.Google Scholar
Mauldin, R. D. and Williams, S. C.. Hausdorff dimension in graph directed constructions. Trans. Amer. Math. Soc. 309 (2) (1988), 811–829.Google Scholar
Patzschke, N. and Zähle, M.. Fractional differentiation in the self-affine case. III. The density of the Cantor set. Proc. Amer. Math. Soc. 117 (1) (1993), 137–144.Google Scholar
Praggastis, B.. Numeration systems and Markov partitions from self similar tilings. Trans. Amer. Math. Soc. 351 (8) (1999), 3315–3349.CrossRefGoogle Scholar
Radin, C. and Wolff, M.. Space tilings and local isomorphism. Geom. Dedicata 42 (3) (1992), 355–360.Google Scholar
Rauzy, G.. Nombres algébriques et substitutions. Bull. Soc. Math. France 110 (2) (1982), 147–178.Google Scholar
Robinson, E. A. Jr. Symbolic dynamics and tilings of ${ \mathbb{R} }^{d} $. Symbolic Dynamics and its Applications (Proceedings of Symposia in Applied Mathematics, 60). American Mathematical Society, Providence, RI, 2004, pp. 81–119.Google Scholar
Schneider, H.. The influence of the marked reduced graph of a nonnegative matrix on the Jordan form and on related properties: a survey. Linear Algebra Appl. 84 (1986), 161–189.Google Scholar
Solomyak, B.. Dynamics of self-similar tilings. Ergod. Th. & Dynam. Sys. 17 (3) (1997), 695–738.Google Scholar
Solomyak, B.. Nonperiodicity implies unique composition for self-similar translationally finite tilings. Discrete Comput. Geom. 20 (1998), 265–279.Google Scholar
Yuasa, H.. Invariant measures for the subshifts arising from non-primitive substitutions. J. Anal. Math. 102 (2007), 143–180.Google Scholar