Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T02:55:20.526Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity, universality, and hyperbolicity of renormalization for critical circle maps with non-integer exponents

Part of: Low-dimensional dynamical systems Complex dynamical systems

Published online by Cambridge University Press:  25 September 2018

IGORS GORBOVICKIS  and
MICHAEL YAMPOLSKY
IGORS GORBOVICKIS
Affiliation:
Jacobs University Bremen, Campus Ring 1, 28759 Bremen, Germany email [email protected]
MICHAEL YAMPOLSKY
Affiliation:
University of Toronto, Mathematics Department, 40 St George Street, Toronto, Ontario, Canada, M5S2E4 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a renormalization operator which acts on analytic circle maps whose critical exponent $\unicode[STIX]{x1D6FC}$ is not necessarily an odd integer 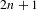$2n+1$, 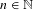$n\in \mathbb{N}$. When 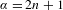$\unicode[STIX]{x1D6FC}=2n+1$, our definition generalizes cylinder renormalization of analytic critical circle maps by Yampolsky [Hyperbolicity of renormalization of critical circle maps. Publ. Math. Inst. Hautes Études Sci.96 (2002), 1–41]. In the case when $\unicode[STIX]{x1D6FC}$ is close to an odd integer, we prove hyperbolicity of renormalization for maps of bounded type. We use it to prove universality and 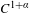$C^{1+\unicode[STIX]{x1D6FC}}$-rigidity for such maps.

Keywords

low-dimensional dynamicsrenormalizationuniversalityrigiditycritical circle map

MSC classification

Primary: 37E20: Universality, renormalization 37F25: Renormalization 37E10: Maps of the circle
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 5 , May 2020 , pp. 1282 - 1334
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bers, L. and Royden, H. L.. Holomorphic families of injections. Acta Math. 157 (1986), 259–286.Google Scholar
Cruz, J. and Smania, D.. Renormalization for critical orders close to $2n$. Preprint, 2010, arXiv:1001.1271.Google Scholar
de Faria, E.. Asymptotic rigidity of scaling ratios for critical circle mappings. Ergod. Th. & Dynam. Sys. 19(4) (1999), 995–1035.Google Scholar
de Faria, E. and de Melo, W.. Rigidity of critical circle mappings I. J. Eur. Math. Soc. 1(4) (1999), 339–392.Google Scholar
de Faria, E. and de Melo, W.. Rigidity of critical circle mappings II. J. Amer. Math. Soc. 13(2) (2000), 343–370.Google Scholar
Douady, A. and Hubbard, J. H.. On the dynamics of polynomial-like mappings. Ann. Sci. Éc. Norm. Supér. (4) 18 (1985), 287–343.Google Scholar
Feigenbaum, M. J., Kadanoff, L. P. and Shenker, S. J.. Quasiperiodicity in dissipative systems: a renormalization group analysis. Physica D 5(2–3) (1982), 370–386.Google Scholar
Guarino, P. and de Melo, W.. Rigidity of smooth critical circle maps. J. Eur. Math. Soc. 19(6) (2017), 1729–1783.Google Scholar
Guarino, P., Martens, M. and de Melo, W.. Rigidity of critical circle maps. Duke Math. J. 167(11) (2018), 2125–2188.Google Scholar
Herman, M.. Conjugaison quasi symétrique des homéomorphismes du cercle à des rotations; Conjugaison quasi symétrique des difféomorphismes du cercle à des rotations et applications aux disques  singuliers de Siegel,  available from http://www.math.kyoto-u.ac.jp/∼mitsu/Herman/index.html, 1986.Google Scholar
Khanin, K. and Teplinsky, A.. Robust rigidity for circle diffeomorphisms with singularities. Invent. Math. 169(1) (2007), 193–218.Google Scholar
Lanford, O. E. III. Renormalization group methods for circle mappings. Statistical Mechanics and Field Theory: Mathematical Aspects (Groningen, 1985) (Lecture Notes in Physics, 257). Springer, Berlin, 1986, pp. 176–189.Google Scholar
Lanford, O. E. III. Renormalization Group Methods for Critical Circle Mappings with General Rotation Number, VIIIth Int. Congress Mathematical Physics (Marseille, 1986). World Scientific, Singapore, 1987, pp. 532–536.Google Scholar
Lanford, O. E. III. Renormalization group methods for circle mappings. Nonlinear Evolution and Chaotic Phenomena (Noto, 1987) (NATO Advanced Science Institute Series B Physics, 176). Plenum, New York, 1988, pp. 25–36.Google Scholar
Lyubich, M.. Investigation of the stability of the dynamics of rational functions. Teor. Funktsii Funktsional. Anal. i Prilozhen. 42 (1984), 72–91 (in Russian). Engl. Trans. Selecta Math. Soviet. 9(1) (1990), 69–90.Google Scholar
Lyubich, M.. Feigenbaum–Coullet–Tresser universality and Milnor’s hairiness conjecture. Ann. of Math. (2) 149 (1999), 319–420.Google Scholar
McMullen, C. T.. Complex Dynamics and Renormalization (Annals of Mathematics Studies, 135). Princeton University Press, Princeton, NJ, 1994.Google Scholar
McMullen, C. T.. Renormalization and 3-Manifolds Which Fiber Over the Circle (Annals of Mathematics Studies, 142). Princeton University Press, Princeton, NJ, 1996.Google Scholar
Mañé, R., Sad, P. and Sullivan, D.. On the dynamics of rational maps. Ann. Sci. Éc. Norm. Supér. (4) 16(2) (1983), 193–217.Google Scholar
Östlund, S., Rand, D., Sethna, J. and Siggia, E.. Universal properties of the transition from quasiperiodicity to chaos in dissipative systems. Physica D 8(3) (1983), 303–342.Google Scholar
Sullivan, D.. Quasiconformal homeomorphisms in dynamics, topology, and geometry. Proc. Int. Congress Mathematicians, Vols. 1, 2 (Berkeley, CA, 1986). American Mathematical Society, Providence, RI, 1987, pp. 1216–1228.Google Scholar
Sullivan, D.. Bounds, quadratic differentials, and renormalization conjectures. American Mathematical Society Centennial Publications, Vol. II (Providence, RI, 1988). American Mathematical Society, Providence, RI, 1992, pp. 417–466.Google Scholar
Yampolsky, M.. Complex bounds for renormalization of critical circle maps. Ergod. Th. & Dynam. Sys. 19 (1999), 227–257.Google Scholar
Yampolsky, M.. The attractor of renormalization and rigidity of towers of critical circle maps. Comm. Math. Phys. 218(3) (2001), 537–568.Google Scholar
Yampolsky, M.. Hyperbolicity of renormalization of critical circle maps. Publ. Math. Inst. Hautes Études Sci. 96 (2002), 1–41.Google Scholar
Yampolsky, M.. Global renormalization horseshoe for critical circle maps. Comm. Math. Phys. 240 (2003), 75–96.Google Scholar
Yampolsky, M.. Renormalization of unicritical analytic circle maps. C.R. Math. Rep. Acad. Sci. Canada 39(3) (2017), 77–89.Google Scholar
Yoccoz, J.-C.. Il n’y a pas de contre-exemple de Denjoy analytique. C. R. Math. Acad. Sci. Paris 298(7) (1984), 141–144.Google Scholar