Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T04:40:46.835Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity for partially hyperbolic diffeomorphisms

Published online by Cambridge University Press:  02 May 2017

RÉGIS VARÃO
RÉGIS VARÃO*
Affiliation:
IMECC-UNICAMP, Rua Sérgio Buarque de Holanda, 651, Campinas, SP, CEP 13083-859, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we completely classify 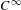$C^{\infty }$ conjugacy for smooth conservative (pointwise) partially hyperbolic diffeomorphisms homotopic to a linear Anosov automorphism on the 3-torus by its center foliation behavior. We prove that the uniform version of absolute continuity for the center foliation is the natural hypothesis to obtain 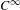$C^{\infty }$ conjugacy to its linear Anosov automorphism. Avila, Viana and Wilkinson [Absolute continuity, Lyapunov exponents and rigidity I: Geodesic flows. J. Eur. Math. Soc. (JEMS)17(6) (2015), 1435–1462] proved that for a perturbation in the volume preserving case of the time-one map of an Anosov flow absolute continuity of the center foliation implies smooth rigidity. The absolute version of absolute continuity is the appropriate scenario for our context since it is not possible to obtain a result analogous to that of Avila, Viana and Wilkinson for our class of maps, for absolute continuity alone fails miserably to imply smooth rigidity for our class of maps. Our theorem is a global rigidity result as we do not assume the diffeomorphism to be at some distance from the linear Anosov automorphism. We also do not assume ergodicity. In particular, a metric condition on the center foliation implies ergodicity and 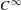$C^{\infty }$ center foliation.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 8 , December 2018 , pp. 3188 - 3200
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anosov, D. V.. Geodesic Flows on Closed Riemann Manifolds with Negative Curvature (Proceedings of the Steklov Institute of Mathematics, 90 (1967)) . American Mathematical Society, Providence, RI, 1969, translated from the Russian by S. Feder.Google Scholar
Avila, A., Viana, M. and Wilkinson, A.. Absolute continuity, Lyapunov exponents and rigidity I: Geodesic flows. J. Eur. Math. Soc. (JEMS) 17(6) (2015), 1435–1462.Google Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102) . Springer, Berlin, 2005.Google Scholar
Brin, M., Burago, D. and Ivanov, S.. On partially hyperbolic diffeomorphisms of 3-manifolds with commutative fundamental group. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 307–312.Google Scholar
Brin, M. and Stuck, G.. Introduction to Dynamical Systems. Cambridge University Press, Cambridge, 2002.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 259) . Springer, London, 2011.Google Scholar
Franks, J.. Anosov diffeomorphisms. Global Analysis (Proc. Sympos. Pure Math., Vol. XIV, Berkeley, CA, 1968) . American Mathematical Society, Providence, RI, 1970, pp. 61–93.Google Scholar
Gogolev, A.. How typical are pathological foliations in partially hyperbolic dynamics: an example. Israel J. Math. 187 (2012), 493–507.Google Scholar
Gogolev, A.. Bootstrap for local rigidity of Anosov automorphisms on the 3-torus. Commun. Math. Phys. (2014), arXiv:1407.7771, accepted.Google Scholar
Hammerlindl, A.. Leaf conjugacies on the torus. Ergod. Th. & Dynam. Sys. 33(3) (2013), 896–933.Google Scholar
Mañé, R.. Contributions to the stability conjecture. Topology 17(4) (1978), 383–396.Google Scholar
Mãné, R.. An ergodic closing lemma. Ann. of Math. (2) 116(3) (1982), 503–540.Google Scholar
Micena, F. and Tahzibi, A.. Regularity of foliations and Lyapunov exponents of partially hyperbolic dynamics on 3-torus. Nonlinearity 26(4) (2013), 1071–1082.Google Scholar
Pesin, Y. B.. Lectures on Partial Hyperbolicity and Stable Ergodicity (Zurich Lectures in Advanced Mathematics) . European Mathematical Society, Zurich, 2004.Google Scholar
Ponce, G., Tahzibi, A. and Varão, R.. Minimal yet measurable foliations. J. Mod. Dyn. 8(1) (2014), 93–107.Google Scholar
Potrie, R.. Partial hyperbolicity and foliations in T3 . J. Mod. Dyn. 9(01) (2015), 81–121.Google Scholar
Pugh, C., Shub, M. and Wilkinson, A.. Hölder foliations. Duke Math. J. 86(3) (1997), 517–546.Google Scholar
Rohlin, V. A.. Lectures on the entropy theory of transformations with invariant measure. Uspekhi Mat. Nauk 22(5(137)) (1967), 3–56.Google Scholar
Ruelle, D. and Wilkinson, A.. Absolutely singular dynamical foliations. Commun. Math. Phys. 219(3) (2001), 481–487.Google Scholar
Shub, M.. Topologically transitive diffeomorphisms of T 4 . Proceedings of the Symposium on Differential Equations and Dynamical Systems (Lecture Notes in Mathematics, 206) . Ed. Chillingworth, D.. Springer, Berlin, 1971.Google Scholar
Ures, R.. Intrinsic ergodicity of partially hyperbolic diffeomorphisms with a hyperbolic linear part. Proc. Amer. Math. Soc. 140(6) (2012), 1973–1985.Google Scholar
Varão, R.. Center foliation: absolute continuity, disintegration and rigidity. Ergod. Th. & Dynam. Sys. 36(1) (2016), 256–275.Google Scholar