Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T05:55:10.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Random local complex dynamics

Part of: Complex dynamical systems Random dynamical systems

Published online by Cambridge University Press:  26 December 2018

LORENZO GUERINI  and
HAN PETERS
LORENZO GUERINI
Affiliation:
University of Amsterdam, Mathematics, Science Park 904, Floor C3, Amsterdam, Netherlands, 1098XH email [email protected], [email protected]
HAN PETERS
Affiliation:
University of Amsterdam, Mathematics, Science Park 904, Floor C3, Amsterdam, Netherlands, 1098XH email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The study of the dynamics of an holomorphic map near a fixed point is a central topic in complex dynamical systems. In this paper, we will consider the corresponding random setting: given a probability measure $\unicode[STIX]{x1D708}$ with compact support on the space of germs of holomorphic maps fixing the origin, we study the compositions 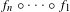$f_{n}\circ \cdots \circ f_{1}$, where each 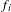$f_{i}$ is chosen independently with probability $\unicode[STIX]{x1D708}$. As in the deterministic case, the stability of the family of the random iterates is mostly determined by the linear part of the germs in the support of the measure. A particularly interesting case occurs when all Lyapunov exponents vanish, in which case stability implies simultaneous linearizability of all germs in 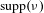$\text{supp}(\unicode[STIX]{x1D708})$.

Keywords

complex dynamicsrandom dynamicslocal dynamics

MSC classification

Primary: 37F50: Small divisors, rotation domains and linearization; Fatou and Julia sets
Secondary: 37H10: Generation, random and stochastic difference and differential equations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 8 , August 2020 , pp. 2156 - 2182
Check for updates
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, M.. Discrete local holomorphic dynamics. Proceedings of 13th Seminar on Analysis and its Applications. Isfahan University Press, Isfahan, 2003, pp. 1–31.Google Scholar
Abate, M.. The residual index and the dynamics of holomorphic maps tangent to the identity. Duke Math. J. 107(1) (2001), 173–207.CrossRefGoogle Scholar
Bracci, F. and Molino, L.. The dynamics near quasi-parabolic fixed points of holomorphic diffeomorphisms in ℂ2. Amer. J. Math. 126(3) (2004), 671–686.CrossRefGoogle Scholar
Bracci, F. and Zaitsev, D.. Dynamics of one-resonant biholomorphisms. J. Eur. Math. Soc. (JEMS) 15(1) (2013), 179–200.CrossRefGoogle Scholar
Brjuno, A. D.. Analytic form of differential equations. I, II. Tr. Mosk. Mat. Obs. 25 (1971), 131–288; ibid. 26 (1972), 199–239.Google Scholar
Cremer, H.. Über die Häufigkeit der Nichtzentren. Math. Ann. 115 (1938), 573–580.CrossRefGoogle Scholar
Duistermaat, J. J. and Kolk, J. A. C.. Lie Groups, 1st edn. Springer, 2000, p. 96.CrossRefGoogle Scholar
Écalle, J.. Les fonctions résurgentes, tome III: L’équation du pont et la classification analytiques des objects locaux. Publ. Math. Orsay 49 (1985), 587 pp.Google Scholar
Engelking, R.. General Topology (Sigma Series in Pure Mathematics, 6), 2nd edn. Heldermann, Berlin, 1989.Google Scholar
Firsova, T., Lyubich, M., Radu, R. and Tanase, R.. Hedgehogs for neutral dissipative germs of holomorphic diffeomorphisms of $(\mathbb{C}^{2},0)$. Preprint, 2016.Google Scholar
Fornaess, J. E. and Sibony, N.. Random iterations of rational functions. Ergod. Th. & Dynam. Sys. 11(4) (1991), 687–708.CrossRefGoogle Scholar
Furstenberg, H. and Kesten, H.. Products of random matrices. Ann. Math. Statist. 31(2) (1960), 457–469.CrossRefGoogle Scholar
Gol’dsheid, I. Y. and Margulis, G. A.. Lyapunov indices of a product of random matrices. Russian Math. Surveys 44(5) (1989), 11–71.CrossRefGoogle Scholar
Grubb, G.. Distribution and Operators (Graduate Texts in Mathematics, 252), 1st edn. Springer, New York, 2009, pp. 9–15.CrossRefGoogle Scholar
Guivarc’h, Y. and Raugi, A.. Frontière de Furstenberg, propriétés de contraction et théorèmes de convergence. Z. Wahrsch. Verw. Gebiete 69(2) (1985), 187–242.CrossRefGoogle Scholar
Hakim, M.. Analytic transformations of (Cp, 0) tangent to the identity. Duke Math. J. 92(2) (1998), 403–428.CrossRefGoogle Scholar
Lattès, S.. Sur les formes réduits des transformations ponctuelles à deux variables. Bulletin de la S.M.F. 39 (1911), 309–345.Google Scholar
Ledrappier, F.. Quelques propriétés des exposants caractéristiques. École d’été de probabilités de Saint-Flour, XII—1982 (Lecture Notes in Mathematics, 1097). Springer, Berlin, 1984, pp. 305–396.CrossRefGoogle Scholar
Lyubich, M., Radu, R. and Tanase, R.. Hedgehogs in higher dimensions and their applications. Preprint, 2016.Google Scholar
Mujica, J.. Spaces of germs of holomorphic functions. Studies in Analysis (Advances in Math. Suppl. Stud., 4). Academic Press, New York, 1979, pp. 1–41.Google Scholar
Oseledec, V. I.. A multiplicative ergodic theorem. Characteristic Ljapunov, exponents of dynamical systems. Tr. Mosk. Mat. Obs. 19 (1968), 179–210.Google Scholar
Poincaré, H.. Oeuvres, Tome I. Gauthier-Villars, Paris, 1928.Google Scholar
Rivi, M.. Parabolic manifolds for semi-attractive holomorphic germs. Michigan Math. J. 49(2) (2001), 211–241.CrossRefGoogle Scholar
Rosay, J.-P. and Rudin, W.. Holomorphic maps from C n to C n. Trans. Amer. Math. Soc. 310(1) (1988), 47–86.Google Scholar
Rudin, W.. Functional Analysis (International Series in Pure and Applied Mathematics, 46-01), 2nd edn. McGraw-Hill Inc., New York, 1991, pp. 149–156.Google Scholar
Ruelle, D.. Ergodic theory of differentiable dynamical systems. Publ. Math. Inst. Hautes Études Sci.(50) (1979), 27–58.CrossRefGoogle Scholar
Siegel, C. L.. Iteration of analytic functions. Ann. of Math. (2) 43 (1942), 607–612.CrossRefGoogle Scholar
Sternberg, S.. Local contractions and a theorem of Poincaré. Amer. J. Math. 79(4) (1957), 809–824.CrossRefGoogle Scholar
Sternberg, S.. On the structure of local homeomorphisms of Euclidean n-space, II. Amer. J. Math. 80(3) (1958), 623–631.CrossRefGoogle Scholar
Stroppel, M.. Locally Compact Groups (EMS Textbooks in Mathematics). European Mathematical Society, Zürich, 2006.CrossRefGoogle Scholar
Sumi, H.. Random complex dynamics and semigroups of holomorphic maps. Proc. Lond. Math. Soc. 102(1) (2011), 50–112.CrossRefGoogle Scholar
Ueda, T.. Local structure of analytic transformations of two complex variables, I. J. Math. Kyoto Univ. 26(2) (1986), 233–261.CrossRefGoogle Scholar
Ueda, T.. Local structure of analytic transformations of two complex variables, II. J. Math. Kyoto Univ. 31(3) (1991), 695–711.CrossRefGoogle Scholar
Viana, M.. Lectures on Lyapunov Exponents (Cambridge Studies in Advanced Mathematics, 145). Cambridge University Press, Cambridge, 2014.CrossRefGoogle Scholar
Yoccoz, J.-C.. Théorème de Siegel, nombres de Bruno et polynômes quadratiques. Astérisque 231 (1995), 3–88.Google Scholar