Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Lin
and
Zhu, Yujun
2015.
Center specification property and entropy for partially hyperbolic diffeomorphisms.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 1,
p.
469.
Sun, Wenxiang
and
Yang, Yun
2016.
Hyperbolic periodic points for chain hyperbolic homoclinic classes.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 7,
p.
3911.
Wang, Lin
2016.
On robustness of orbit spaces for partially hyperbolic endomorphisms.
Chinese Annals of Mathematics, Series B,
Vol. 37,
Issue. 6,
p.
899.
Zhang, Fang
and
Zhou, Yunhua
2017.
On the limit quasi-shadowing property.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 5,
p.
2861.
Wang, Lin
Wang, Xin Sheng
and
Zhu, Yu Jun
2018.
Quasi-shadowing Property on Random Partially Hyperbolic Sets.
Acta Mathematica Sinica, English Series,
Vol. 34,
Issue. 9,
p.
1429.
Backes, Lucas
and
Dragičević, Davor
2020.
Quasi-shadowing for partially hyperbolic dynamics on Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 492,
Issue. 1,
p.
124445.
Li, Zhiping
and
Zhou, Yunhua
2020.
Quasi-shadowing and limit quasi-shadowing for quasi-partially hyperbolic strings of flows.
Journal of Differential Equations,
Vol. 269,
Issue. 12,
p.
11062.
Castro, A.
Rodrigues, F.
and
Varandas, P.
2020.
Leafwise shadowing property for partially hyperbolic diffeomorphisms.
Dynamical Systems,
Vol. 35,
Issue. 2,
p.
306.
Backes, Lucas
and
Dragičević, Davor
2021.
A general approach to nonautonomous shadowing for nonlinear dynamics.
Bulletin des Sciences Mathématiques,
Vol. 170,
Issue. ,
p.
102996.
Pan, Juan
Zhang, Wenda
and
Zhou, Yunhua
2021.
Shadowing properties for weakly hyperbolic Zd-actions.
Journal of Mathematical Analysis and Applications,
Vol. 496,
Issue. 2,
p.
124814.
Lin, Wang
Xinsheng, Wang
and
Yujun, Zhu
2022.
Subsystems with the shadowing 性质 for bm$\mathbb{Z}^{k}$-actions.
SCIENTIA SINICA Mathematica,
Vol. 52,
Issue. 10,
p.
1145.
Carrasco-Olivera, D.
Lee, K.
Morales, C. A.
and
Villavicencio, H.
2022.
Finite-Expansivity and N-Shadowing.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 53,
Issue. 1,
p.
107.
Lee, Manseob
and
Ahn, Jiweon
2022.
Partial hyperbolicity and pseudo orbit tracing properties.
Topology and its Applications,
Vol. 314,
Issue. ,
p.
108095.
Tian, Xueting
and
Wu, Weisheng
2022.
Unstable entropies and dimension theory of partially hyperbolic systems.
Nonlinearity,
Vol. 35,
Issue. 1,
p.
658.
Al-Ftlawy, Dunia M.K.
and
Al-Shara'a, Iftichar M.T.
2023.
Center Fitting Shadowing Property for Partial Hyperbolic Diffeomorphisms.
p.
01.
Wang, Lin
Wang, Xinsheng
and
Wang, Lei
2023.
Measurable Versions of Some Topological Properties for Diffeomorphisms with Continuous Foliations.
Mathematical Problems in Engineering,
Vol. 2023,
Issue. 1,
Wang, Lin
2023.
Quasi-Shadowing for Partially Hyperbolic Flows with a Local Product Structure.
Journal of Dynamical and Control Systems,
Vol. 29,
Issue. 1,
p.
95.
SHI, YI
and
WANG, XIAODONG
2024.
-chain closing lemma for certain partially hyperbolic diffeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 44,
Issue. 7,
p.
1923.
Ren, Xiankun
and
Zhou, Yunhua
2024.
Shadowing for nonuniformly hyperbolic maps in Hilbert spaces.
Nonlinearity,
Vol. 37,
Issue. 5,
p.
055008.
Pan, Juan
Ren, Xian Kun
and
Zhou, Yun Hua
2024.
Quasi-shadowing for ℤd-actions.
Acta Mathematica Sinica, English Series,
Vol. 40,
Issue. 6,
p.
1563.
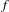 $f$ has the quasi-shadowing property if for any pseudo orbit
$f$ has the quasi-shadowing property if for any pseudo orbit 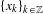 $\{x_{k}\}_{k\in \mathbb{Z}}$, there is a sequence of points
$\{x_{k}\}_{k\in \mathbb{Z}}$, there is a sequence of points 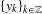 $\{y_{k}\}_{k\in \mathbb{Z}}$ tracing it in which
$\{y_{k}\}_{k\in \mathbb{Z}}$ tracing it in which 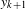 $y_{k+1}$ is obtained from
$y_{k+1}$ is obtained from 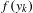 $f(y_{k})$ by a motion
$f(y_{k})$ by a motion  ${\it\tau}$ along the center direction. We show that any partially hyperbolic diffeomorphism has the quasi-shadowing property, and if
${\it\tau}$ along the center direction. We show that any partially hyperbolic diffeomorphism has the quasi-shadowing property, and if 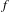 $f$ has a
$f$ has a 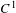 $C^{1}$ center foliation then we can require
$C^{1}$ center foliation then we can require  ${\it\tau}$ to move the points along the center foliation. As applications, we show that any partially hyperbolic diffeomorphism is topologically quasi-stable under
${\it\tau}$ to move the points along the center foliation. As applications, we show that any partially hyperbolic diffeomorphism is topologically quasi-stable under 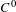 $C^{0}$-perturbation. When
$C^{0}$-perturbation. When 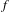 $f$ has a uniformly compact
$f$ has a uniformly compact  $C^{1}$ center foliation, we also give partially hyperbolic diffeomorphism versions of some theorems which hold for uniformly hyperbolic systems, such as the Anosov closing lemma, the cloud lemma and the spectral decomposition theorem.
$C^{1}$ center foliation, we also give partially hyperbolic diffeomorphism versions of some theorems which hold for uniformly hyperbolic systems, such as the Anosov closing lemma, the cloud lemma and the spectral decomposition theorem.