Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-30T15:28:16.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Pure point/continuous decomposition of translation-bounded measures and diffraction

Published online by Cambridge University Press:  10 July 2018

JEAN-BAPTISTE AUJOGUE
JEAN-BAPTISTE AUJOGUE*
Affiliation:
Institut Camille Jordan, Mathematics, 43 boulevard du 11 novembre 1918, 69622 Villeurbanne cedex, Lyon 69622, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we consider translation-bounded measures over a locally compact Abelian group 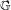$\mathbb{G}$, with a particular interest in their so-called diffraction. Given such a measure $\unicode[STIX]{x1D714}$, its diffraction 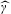$\widehat{\unicode[STIX]{x1D6FE}}$ is another measure on the Pontryagin dual 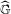$\widehat{\mathbb{G}}$, whose decomposition into the sum 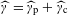$\widehat{\unicode[STIX]{x1D6FE}}=\widehat{\unicode[STIX]{x1D6FE}}_{\text{p}}+\widehat{\unicode[STIX]{x1D6FE}}_{\text{c}}$ of its atomic and continuous parts is central in diffraction theory. The problem we address here is whether the above decomposition of 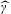$\widehat{\unicode[STIX]{x1D6FE}}$ lifts to $\unicode[STIX]{x1D714}$ itself, that is to say, whether there exists a decomposition 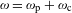$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}+\unicode[STIX]{x1D714}_{\text{c}}$, where 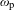$\unicode[STIX]{x1D714}_{\text{p}}$ and 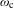$\unicode[STIX]{x1D714}_{\text{c}}$ are translation-bounded measures having diffraction 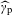$\widehat{\unicode[STIX]{x1D6FE}}_{\text{p}}$ and 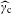$\widehat{\unicode[STIX]{x1D6FE}}_{\text{c}}$, respectively. Our main result here is the almost sure existence, in a sense to be made precise, of such a decomposition. It will also be proved that a certain uniqueness property holds for the above decomposition. Next, we will be interested in the situation where translation-bounded measures are weighted Meyer sets. In this context, it will be shown that the decomposition, whether it exists, also consists of weighted Meyer sets. We complete this work by discussing a natural generalization of the considered problem.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 2 , February 2020 , pp. 309 - 352
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Argabright, L. N. and De Lamadrid, J. G.. Fourier Analysis of Unbounded Measures on Locally Compact Abelian Groups (Memoirs of the American Mathematical Society, 145) . American Mathematical Soceity, Providence, RI, 1974.Google Scholar
Aujogue, J.-B.. On embedding of repetitive Meyer multiple sets into model multiple sets. Ergod. Th. & Dynam. Sys. 36(6) (2015), 1679–1702.Google Scholar
Aujogue, J.-B., Barge, M., Kellendonk, J. and Lenz, D.. Equicontinuous factors, proximality and Ellis semigroup for delone sets. Mathematics of Aperiodic Order. Springer, Basel, 2015, pp. 137–194.Google Scholar
Baake, M.. Diffraction of weighted lattice subsets. Canad. Math. Bull. 45 (2002), 483–498.Google Scholar
Baake, M.. Mathematical diffraction theory in Euclidian spaces. Lecture Notes, Troisième cycle de la physique en Suisse romande, EPFL, Lausanne, 2005.Google Scholar
Baake, M., Birkner, M. and Grimm, U.. Non-periodic systems with continuous diffraction measures. Mathematics of Aperiodic Order. Springer, Basel, 2015, pp. 1–32.Google Scholar
Baake, M., Birkner, M. and Moody, R. V.. Diffraction of stochastic point sets: explicitly computable examples. Comm. Math. Phys. 293(3) (2010), 611–660.Google Scholar
Baake, M., Gähler, F. and Grimm, U.. Examples of substitution systems and their factors. J. Integer Seq. 16(2) (2013), 3.Google Scholar
Baake, M. and Grimm, U.. Mathematical diffraction of aperiodic structures. Chem. Soc. Rev. 41(20) (2012), 6821–6843.Google Scholar
Baake, M. and Grimm, U.. Aperiodic Order, Vol. 1. Cambridge University Press, Cambridge, 2013.Google Scholar
Baake, M. and Grimm, U.. Squirals and beyond: substitution tilings with singular continuous spectrum. Ergod. Th. & Dynam. Sys. 34(04) (2014), 1077–1102.Google Scholar
Baake, M., Hermisson, J. and Pleasants, P. A. B.. The torus parametrization of quasiperiodic Li-classes. J. Phys. A 30(9) (1997), 3029.Google Scholar
Baake, M. and Lenz, D.. Dynamical systems on translation bounded measures: pure point dynamical and diffraction spectra. Ergod. Th. & Dynam. Sys. 24(06) (2004), 1867–1893.Google Scholar
Baake, M., Lenz, D. and Moody, R. V.. Characterization of model sets by dynamical systems. Ergod. Th. & Dynam. Sys. 27(02) (2007), 341–382.Google Scholar
Baake, M., Lenz, D. and van Enter, A.. Dynamical versus diffraction spectrum for structures with finite local complexity. Ergod. Th. & Dynam. Sys. 35(7) (2015), 2017–2043.Google Scholar
Baake, M. and Moody, R. V.. Diffractive point sets with entropy. J. Phys. A 31(45) (1998), 9023.Google Scholar
Baake, M. and Moody, R. V.. Weighted Dirac combs with pure point diffraction. J. Reine Angew. Math. 573 (2004), 61–94.Google Scholar
Baake, M., Moody, R. V. and Schlottmann, M.. Limit-(quasi) periodic point sets as quasicrystals with p-adic internal spaces. J. Phys. A 31(27) (1998), 5755.Google Scholar
Baake, M. and Zint, N.. Absence of singular continuous diffraction for discrete multi-component particle models. J. Stat. Phys. 130(4) (2008), 727–740.Google Scholar
Chang, J. T. and Pollard, D.. Conditioning as disintegration. Stat. Neerl. 51(3) (1997), 287–317.Google Scholar
De Lamadrid, J. G. and Argabright, L. N.. Almost Periodic Measures (Memoirs of the American Mathematical Society, 428) . American Mathematical Soceity, Providence, RI, 1990.Google Scholar
Deng, X. and Moody, R. V.. Dworkin’s argument revisited: point processes, dynamics, diffraction, and correlations. J. Geom. Phys. 58(4) (2008), 506–541.Google Scholar
Dworkin, S.. Spectral theory and x-ray diffraction. J. Math. Phys. 34(7) (1993), 2965–2967.Google Scholar
Fell, J. M. G. and Doran, R. S.. Representations of *-Algebras, Locally Compact Groups, and Banach *-Algebraic Bundles: Banach *-Algebraic Bundles, Induced Representations, and the Generalized Mackey Analysis (Pure and Applied Mathematics) . Elsevier Science, Amsterdam, 1988.Google Scholar
Feres, R. and Katok, A.. Ergodic Theory and Dynamics of g-spaces (Handbook of Dynamical Systems, 1) . Elsevier Science, Amsterdam, 2002, pp. 665–763.Google Scholar
Forrest, A., Hunton, J. and Kellendonk, J.. Topological Invariants for Projection Method Patterns (Memoirs of the American Mathematical Society, 758) . American Mathematical Soceity, Providence, RI, 2002.Google Scholar
Furstenberg, H. and Katznelson, Y.. Idempotents in compact semigroups and Ramsey theory. Israel J. Math. 68(3) (1989), 257–270.Google Scholar
Gouéré, J.-B.. Diffraction et mesure de palm des processus ponctuels. C. R. Math. 336(1) (2003), 57–62.Google Scholar
Gouéré, J.-B.. Quasicrystals and almost periodicity. Comm. Math. Phys. 255(3) (2005), 655–681.Google Scholar
Grimm, U. and Baake, M.. Homometric point sets and inverse problems. Z. Kristallographie 223(11–12) (2008), 777–781.Google Scholar
Hof, A.. On diffraction by aperiodic structures. Comm. Math. Phys. 169(1) (1995), 25–43.Google Scholar
Huck, C. and Richard, C.. On pattern entropy of weak model sets. Discrete Comput. Geom. 54(3) (2015), 741–757.Google Scholar
Kelley, J. L.. General Topology. Springer, New York, 1975.Google Scholar
Lagarias, J. C.. Meyer’s concept of quasicrystal and quasiregular sets. Comm. Math. Phys. 179(2) (1996), 365–376.Google Scholar
Lagarias, J. C.. Geometric models for quasicrystals i. Delone sets of finite type. Discrete Comput. Geom. 21(2) (1999), 161–191.Google Scholar
Lee, J.-Y. and Moody, R. V.. A characterization of model multi-colour sets. Ann. Henri Poincaré 7(1) (2006), 125–143.Google Scholar
Lee, J.-Y., Moody, R. V. and Solomyak, B.. Pure point dynamical and diffraction spectra. Ann. Henri Poincaré 3(5) (2002), 1003–1018.Google Scholar
Lenz, D. and Moody, R. V.. Stationary processes and pure point diffraction. Ergod. Th. & Dynam. Sys. (2016), 1–46.Google Scholar
Lenz, D. and Richard, C.. Pure point diffraction and cut and project schemes for measures: the smooth case. Math. Z. 256(2) (2007), 347–378.Google Scholar
Lindenstrauss, E.. Pointwise theorems for amenable groups. Invent. Math. 146(2) (2001), 259–295.Google Scholar
Loomis, L. H.. Introduction to Abstract Harmonic Analysis (Dover Books on Mathematics) . Dover, New York, 2011.Google Scholar
Meyer, Y.. Algebraic Numbers and Harmonic Analysis (North-Holland Mathematical Library) . North-Holland, Amsterdam, 1972.Google Scholar
Meyer, Y.. Quasicrystals, diophantine approximation and algebraic numbers. Beyond Quasicrystals. Springer, Berlin, 1995, pp. 3–16.Google Scholar
Moody, R. V.. Meyer sets and the finite generation of quasicrystals. Symmetries in Science VIII. Springer, Boston, MA, 1995, pp. 379–394.Google Scholar
Moody, R. V.. Meyer sets and their duals. NATO ASI Series C Math. Phys. Sci. 489 (1997), 403–442.Google Scholar
Moody, R. V.. Model sets: a survey. From Quasicrystals to More Complex Systems (Centre de Physique des Houches, 13) . Springer, Berlin, 2000, pp. 145–166.Google Scholar
Moody, R. V.. Uniform distribution in model sets. Canad. Math. Bull. 45(1) (2002), 123–130.Google Scholar
Müller, P. and Richard, C.. Ergodic properties of randomly coloured point sets. Canad. J. Math. 65 (2013), 349–402.Google Scholar
Reed, M. and Simon, B.. Methods of Modern Mathematical Physics: Functional Analysis, Vol. 1. Gulf Professional Publishing, Houston, TX, 1980.Google Scholar
Richard, C.. Dense Dirac combs in euclidean space with pure point diffraction. J. Math. Phys. 44(10) (2003), 4436–4449.Google Scholar
Rudin, W.. Fourier Analysis on Groups, Vol. 12. John Wiley & Sons, 1990.Google Scholar
Rudin, W.. Functional Analysis (International Series in Pure and Applied Mathematics) . McGraw-Hill, New York, 1991.Google Scholar
Schlotmann, M.. Cut-and-project sets in locally compact abelian groups. Quasicrystals and Discrete Geometry (Fields Institute Monographs, 10) . American Mathematical Society, Providence, RI, 1998, pp. 247–264.Google Scholar
Schlottmann, M.. Generalized model sets and dynamical systems. Directions in Mathematical Quasicrystals (CRM Monograph series, 13) . American Mathematical Society, Providence, RI, 2000, pp. 143–159.Google Scholar
Shechtman, D., Blech, I., Gratias, D. and Cahn, J. W.. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53(20) (1984), 1951.Google Scholar
Struble, R. A.. Metrics in locally compact groups. Compos. Math. 28(3) (1974), 217–222.Google Scholar
Strungaru, N.. On weighted Dirac combs supported inside model sets. J. Phys. A 47(33) (2014), 335202.Google Scholar
Strungaru, N.. Almost periodic measures and Meyer sets. Preprint, 2015, arXiv:1501.00945.Google Scholar
Terauds, V.. The inverse problem of pure point diffraction – examples and open questions. J. Stat. Phys. 152(5) (2013), 954–968.Google Scholar
van Den Berg, C. and Forst, G.. Potential Theory on Locally Compact Abelian Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, 87) . Springer Science & Business Media, Berlin, 2012.Google Scholar