Article contents
Point transitivity, 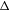 ${\rm\Delta}$-transitivity and multi-minimality
${\rm\Delta}$-transitivity and multi-minimality
Published online by Cambridge University Press: 14 March 2014
Abstract
Let 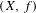 $(X,f)$ be a topological dynamical system and
$(X,f)$ be a topological dynamical system and 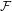 ${\mathcal{F}}$ be a Furstenberg family (a collection of subsets of
${\mathcal{F}}$ be a Furstenberg family (a collection of subsets of  $\mathbb{N}$ with hereditary upward property). A point
$\mathbb{N}$ with hereditary upward property). A point 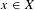 $x\in X$ is called an
$x\in X$ is called an 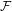 ${\mathcal{F}}$-transitive point if for every non-empty open subset
${\mathcal{F}}$-transitive point if for every non-empty open subset 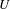 $U$ of
$U$ of 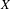 $X$ the entering time set of
$X$ the entering time set of  $x$ into
$x$ into 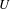 $U$,
$U$, 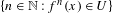 $\{n\in \mathbb{N}:f^{n}(x)\in U\}$, is in
$\{n\in \mathbb{N}:f^{n}(x)\in U\}$, is in 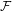 ${\mathcal{F}}$; the system
${\mathcal{F}}$; the system  $(X,f)$ is called
$(X,f)$ is called 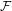 ${\mathcal{F}}$-point transitive if there exists some
${\mathcal{F}}$-point transitive if there exists some 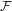 ${\mathcal{F}}$-transitive point. In this paper, we first discuss the connection between
${\mathcal{F}}$-transitive point. In this paper, we first discuss the connection between 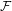 ${\mathcal{F}}$-point transitivity and
${\mathcal{F}}$-point transitivity and 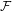 ${\mathcal{F}}$-transitivity, and show that weakly mixing and strongly mixing systems can be characterized by
${\mathcal{F}}$-transitivity, and show that weakly mixing and strongly mixing systems can be characterized by 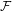 ${\mathcal{F}}$-point transitivity, completing results in [Transitive points via Furstenberg family. Topology Appl. 158 (2011), 2221–2231]. We also show that multi-transitivity,
${\mathcal{F}}$-point transitivity, completing results in [Transitive points via Furstenberg family. Topology Appl. 158 (2011), 2221–2231]. We also show that multi-transitivity, 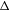 ${\rm\Delta}$-transitivity and multi-minimality can be characterized by
${\rm\Delta}$-transitivity and multi-minimality can be characterized by 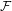 ${\mathcal{F}}$-point transitivity, answering two questions proposed by Kwietniak and Oprocha [On weak mixing, minimality and weak disjointness of all iterates. Ergod. Th. & Dynam. Sys. 32 (2012), 1661–1672].
${\mathcal{F}}$-point transitivity, answering two questions proposed by Kwietniak and Oprocha [On weak mixing, minimality and weak disjointness of all iterates. Ergod. Th. & Dynam. Sys. 32 (2012), 1661–1672].
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 13
- Cited by


