Article contents
The Pisot conjecture for 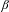 $\unicode[STIX]{x1D6FD}$-substitutions
$\unicode[STIX]{x1D6FD}$-substitutions
Published online by Cambridge University Press: 22 September 2016
Abstract
We prove the Pisot conjecture for 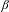 $\unicode[STIX]{x1D6FD}$-substitutions: if
$\unicode[STIX]{x1D6FD}$-substitutions: if 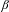 $\unicode[STIX]{x1D6FD}$ is a Pisot number, then the tiling dynamical system
$\unicode[STIX]{x1D6FD}$ is a Pisot number, then the tiling dynamical system 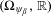 $(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}},\mathbb{R})$ associated with the
$(\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D6FD}}},\mathbb{R})$ associated with the 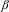 $\unicode[STIX]{x1D6FD}$-substitution has pure discrete spectrum. As corollaries: (1) arithmetical coding of the hyperbolic solenoidal automorphism associated with the companion matrix of the minimal polynomial of any Pisot number is almost everywhere one-to-one; and (2) all Pisot numbers are weakly finitary.
$\unicode[STIX]{x1D6FD}$-substitution has pure discrete spectrum. As corollaries: (1) arithmetical coding of the hyperbolic solenoidal automorphism associated with the companion matrix of the minimal polynomial of any Pisot number is almost everywhere one-to-one; and (2) all Pisot numbers are weakly finitary.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 6
- Cited by


