Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T01:08:12.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Orbit growth for algebraic flip systems

Published online by Cambridge University Press:  07 August 2014

RICHARD MILES
RICHARD MILES*
Affiliation:
School of Mathematics, University of East Anglia, Norwich, NR4 7TJ, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An algebraic flip system is an action of the infinite dihedral group by automorphisms of a compact abelian group 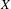$X$. In this paper, a fundamental structure theorem is established for irreducible algebraic flip systems, that is, systems for which the only closed invariant subgroups of 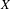$X$ are finite. Using irreducible systems as a foundation, for expansive algebraic flip systems, periodic point counting estimates are obtained that lead to the orbit growth estimate

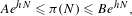$$\begin{eqnarray}Ae^{hN}\leqslant {\it\pi}(N)\leqslant Be^{hN},\end{eqnarray}$$
where ${\it\pi}(N)$ denotes the number of orbits of length at most 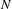$N$, $A$ and $B$ are positive constants and 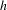$h$ is the topological entropy.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 8 , December 2015 , pp. 2613 - 2631
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V. I.. Reversible systems. Nonlinear and Turbulent Processes in Physics, Vol. 3 (Kiev, 1983). Harwood Academic Publ, Chur, 1984, pp. 1161–1174.Google Scholar
Böttcher, A. and Grudsky, S. M.. Spectral Properties of Banded Toeplitz Matrices. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2005.CrossRefGoogle Scholar
Bowen, R.. Some systems with unique equilibrium states. Math. Systems Theory 8(3) (1974/75), 193–202.CrossRefGoogle Scholar
Crapo, H.. Möbius inversion in lattices. Arch. Math. 19 (1968), 595–607.CrossRefGoogle Scholar
Devaney, R. L.. Reversible diffeomorphisms and flows. Trans. Amer. Math. Soc. 218 (1976), 89–113.CrossRefGoogle Scholar
Einsiedler, M. and Rindler, H.. Algebraic actions of the discrete Heisenberg group and other non-abelian groups. Aequationes Math. 62(1–2) (2001), 117–135.CrossRefGoogle Scholar
Eisenbud, D.. Commutative Algebra: With a View Toward Algebraic Geometry (Graduate Texts in Mathematics, 150). Springer, New York, 1995.CrossRefGoogle Scholar
Everest, G., Miles, R., Stevens, S. and Ward, T.. Orbit-counting in non-hyperbolic dynamical systems. J. Reine Angew. Math. 608 (2007), 155–182.Google Scholar
Everest, G., Miles, R., Stevens, S. and Ward, T.. Dirichlet series for finite combinatorial rank dynamics. Trans. Amer. Math. Soc. 362(1) (2010), 199–227.CrossRefGoogle Scholar
Goodson, G. R., del Junco, A., Lemańczyk, M. and Rudolph, D. J.. Ergodic transformations conjugate to their inverses by involutions. Ergod. Th. & Dynam. Sys. 16(1) (1996), 97–124.CrossRefGoogle Scholar
Hawkes, T., Isaacs, I. M. and Özaydin, M.. On the Möbius function of a finite group. Rocky Mountain J. Math. 19(4) (1989), 1003–1034.CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis: Structure of topological groups, integration theory, group representations, Vol. I (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 115), 2nd edn. Springer, Berlin, 1979.CrossRefGoogle Scholar
Kim, Y., Lee, J. and Park, K.. A zeta function for flip systems. Pacific J. Math. 209(2) (2003), 289–301.CrossRefGoogle Scholar
Lind, D., Schmidt, K. and Ward, T.. Mahler measure and entropy for commuting automorphisms of compact groups. Invent. Math. 101(3) (1990), 593–629.CrossRefGoogle Scholar
Lind, D. A.. A zeta function for Zd -actions. Ergodic Theory of Zd Actions (Warwick, 1993–1994) (London Mathematical Society Lecture Note Series, 228). Cambridge University Press, Cambridge, 1996, pp. 433–450.Google Scholar
Margulis, G. A.. On Some Aspects of the Theory of Anosov Systems (Springer Monographs in Mathematics). Springer, Berlin, 2004, with a survey by R Sharp: periodic orbits of hyperbolic flows, translated from the Russian by Valentina Vladimirovna Szulikowska.CrossRefGoogle Scholar
Miles, R.. Periodic points of endomorphisms on solenoids and related groups. Bull. Lond. Math. Soc. 40(4) (2008), 696–704.CrossRefGoogle Scholar
Miles, R. and Ward, T.. Orbit-counting for nilpotent group shifts. Proc. Amer. Math. Soc. 137(4) (2009), 1499–1507.CrossRefGoogle Scholar
Miles, R. and Ward, T.. A dichotomy in orbit growth for commuting automorphisms. J. Lond. Math. Soc. (2) 81(3) (2010), 715–726.CrossRefGoogle Scholar
Parry, W. and Pollicott, M.. An analogue of the prime number theorem for closed orbits of Axiom A flows. Ann. of Math. (2) 118(3) (1983), 573–591.CrossRefGoogle Scholar
Parry, W.. An analogue of the prime number theorem for closed orbits of shifts of finite type and their suspensions. Israel J. Math. 45(1) (1983), 41–52.CrossRefGoogle Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin (Progress in Mathematics, 128). Birkhäuser, Basel, 1995.Google Scholar
Schmidt, K.. Algebra, arithmetic and multi-parameter ergodic theory. Internat. Math. Nachrichten 200 (2005), 1–21.Google Scholar
Sevryuk, M. B.. Reversible Systems (Lecture Notes in Mathematics, 1211). Springer, Berlin, 1986.CrossRefGoogle Scholar
Sinaĭ, Ja. G.. Asymptotic behavior of closed geodesics on compact manifolds with negative curvature. Izv. Akad. Nauk SSSR Ser. Mat. 30 (1966), 1275–1296.Google Scholar
Stanley, R. P.. Enumerative Combinatorics, Vol. 1 (Cambridge Studies in Advanced Mathematics, 49). Cambridge University Press, Cambridge, 1997, with a foreword by Gian-Carlo Rota, corrected reprint of the 1986 original.CrossRefGoogle Scholar
Waddington, S.. The prime orbit theorem for quasihyperbolic toral automorphisms. Monatsh. Math. 112(3) (1991), 235–248.CrossRefGoogle Scholar
Wehrfritz, B. A. F.. Group and Ring Theoretic Properties of Polycyclic Groups (Algebra and Applications, 10). Springer, London, 2009.CrossRefGoogle Scholar