Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T04:06:12.415Z Has data issue: false hasContentIssue false
  • English
  • Français

On the trigonometric moment problem

Published online by Cambridge University Press:  16 November 2012

AMELIA ÁLVAREZ ,
JOSÉ LUIS BRAVO  and
COLIN CHRISTOPHER
AMELIA ÁLVAREZ
Affiliation:
Departamento de Matemáticas, Universidad de Extremadura, Avda. Elvas s/n, 06006 Badajoz, Spain (email: [email protected])
JOSÉ LUIS BRAVO
Affiliation:
Departamento de Matemáticas, Universidad de Extremadura, Avda. Elvas s/n, 06006 Badajoz, Spain (email: [email protected])
COLIN CHRISTOPHER
Affiliation:
School of Computing and Mathematics (Faculty of Science and Technology), University of Plymouth, Room 9, 2 Kirkby Place, Drake Circus, Plymouth, Devon, PL4 8AA, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

The trigonometric moment problem arises from the study of one-parameter families of centers in polynomial vector fields. It seeks to classify the trigonometric polynomials 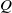$Q$ which are orthogonal to all powers of a trigonometric polynomial 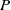$P$. We show that this problem has a simple and natural solution under certain conditions on the monodromy group of the Laurent polynomial associated to $P$. In the case of real trigonometric polynomials, which is the primary motivation of the problem, our conditions are shown to hold for all trigonometric polynomials of degree 15 or less. In the complex case, we show that there are a small number of exceptional monodromy groups up to degree 30 where the conditions fail to hold and show how counterexamples can be constructed in several of these cases.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 1 , February 2014 , pp. 1 - 20
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Álvarez, A., Bravo, J. L. and Mardešić, P.. Vanishing abelian integrals on zero-dimensional cycles. Preprint, arXiv:1101.1777v2.Google Scholar
[2]Briskin, M., Françoise, J. P. and Yomdin, Y.. Center conditions, compositions of polynomials and moments on algebraic curves. Ergod. Th. & Dynam. Sys. 19(5) (1999), 1201–1220.Google Scholar
[3]Briskin, M., Françoise, J. P. and Yomdin, Y.. Center conditions II: Parametric and model center problems. Israel J. Math. 118 (2000), 61–82.Google Scholar
[4]Briskin, M., Roytvarf, N. and Yomdin, Y.. Center conditions at infinity for Abel differential equation. Ann. of Math. (2) 172 (2010), 437–483.Google Scholar
[5]Cherkas, L. A.. Number of limit cycles of an autonomous second-order system. Differ. Uravn. 12 (1975), 944–946.Google Scholar
[6]Christopher, C.. Abel equations: composition conjectures and the model problem. Bull. Lond. Math. Soc. 32(3) (2000), 332–338.Google Scholar
[7]Christopher, C. and Mardešić, P.. The monodromy problem and the tangential center problem. Funktsional. Anal. i Prilozhen. 44(1) (2010), 27–43.Google Scholar
[8]Françoise, J. P., Pakovich, F., Yomdin, Y. and Zhao, W.. Moment vanishing problem and positivity: some examples. Bull. Sci. Math. 135(1) (2011), 10–32.Google Scholar
[9]The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.4.10; 2007, http://www.gap-system.org.Google Scholar
[10]Gavrilov, L. and Movasati, H.. The infinitesimal 16th Hilbert problem in dimension zero. Bull. Sci. Math. 131 (2007), 242–257.Google Scholar
[11]Gavrilov, L. and Pakovich, F.. Moments on Riemann surfaces and hyperelliptic Abelian integrals. Preprint, 15 July 2011, arXiv:1107.3029v1.Google Scholar
[12]Malle, G. and Matzat, H.. Inverse Galois Theory. Springer, Berlin, 1999.Google Scholar
[13]Pakovich, F.. Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem. Preprint, arXiv:0908.2508v3.Google Scholar
[14]Pakovich, F.. On polynomials orthogonal to all powers of a given polynomial on a segment. Israel J. Math. 142 (2004), 273–283.Google Scholar
[15]Pakovich, F.. On rational functions orthogonal to all powers of a given rational function on a curve. Preprint, arXiv:0910.2105v1.Google Scholar
[16]Pakovich, F.. Prime and composite Laurent polynomials. Bull. Sci. Math. 133(7) (2009), 693–732.Google Scholar
[17]Pakovich, F. and Muzychuk, M.. Solution of the polynomial moment problem. Proc. Lond. Math. Soc. 99(3) (2009), 633–657.Google Scholar
[18]Pakovich, F., Pech, C. and Zvonkin, A. K.. Laurent polynomial moment problem: a case study. Contemp. Math. 532 (2010), 177–194.Google Scholar
[19]Pakovich, F., Roytvarf, N. and Yomdin, Y.. Cauchy type integrals of algebraic functions. Israel J. Math. 144 (2004), 221–291.Google Scholar
[20]Scott, W. R.. Group Theory. Dover, New York, 1987.Google Scholar
[21]van der Waerden, B. L.. Algebra. Vol. 1. Frederick Ungar, New York, 1970.Google Scholar
[22]Wielandt, H.. Finite Permutation Groups. Academic Press, New York, 1964.Google Scholar
[23]Zieve, M. E.. Decompositions of Laurent polynomials. Preprint, arXiv:0710.1902v1.Google Scholar
[24]Żołądek, H.. The Monodromy Group (Mathematics Institute of the Polish Academy of Science, Mathematical Monographs (New Series), 67). Birkhäuser, Basel, 2006.Google Scholar