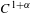Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bonatti, C.
Monteverde, I.
Navas, A.
and
Rivas, C.
2017.
Rigidity for $$C^1$$ C 1 actions on the interval arising from hyperbolicity I: solvable groups.
Mathematische Zeitschrift,
Vol. 286,
Issue. 3-4,
p.
919.
Kim, Sang-hyun
and
Koberda, Thomas
2018.
Free products and the algebraic structure of diffeomorphism groups.
Journal of Topology,
Vol. 11,
Issue. 4,
p.
1054.
Kim, Sang-hyun
and
Koberda, Thomas
2020.
Diffeomorphism groups of critical regularity.
Inventiones mathematicae,
Vol. 221,
Issue. 2,
p.
421.
Kim, Sang-hyun
Koberda, Thomas
and
Rivas, Cristóbal
2021.
Direct products, overlapping actions, and critical regularity.
Journal of Modern Dynamics,
Vol. 17,
Issue. 0,
p.
285.
Kim, Sang-hyun
Koberda, Thomas
and
Rivas, Cristóbal
2024.
Virtual Critical Regularity of Mapping Class Group Actions on the Circle.
Transformation Groups,
Vol. 29,
Issue. 3,
p.
1105.