Hostname: page-component-f554764f5-qhdkw Total loading time: 0 Render date: 2025-04-20T06:29:18.171Z Has data issue: false hasContentIssue false
  • English
  • Français

On the quasi-ergodicity of absorbing Markov chains with unbounded transition densities, including random logistic maps with escape

Part of: Random dynamical systems Special classes of linear operators Markov processes

Published online by Cambridge University Press:  25 September 2023

MATHEUS M. CASTRO Open the ORCID record for MATHEUS M. CASTRO [Opens in a new window] ,
VINCENT P. H. GOVERSE Open the ORCID record for VINCENT P. H. GOVERSE [Opens in a new window] ,
JEROEN S. W. LAMB Open the ORCID record for JEROEN S. W. LAMB [Opens in a new window]  and
MARTIN RASMUSSEN Open the ORCID record for MARTIN RASMUSSEN [Opens in a new window]
MATHEUS M. CASTRO*
Affiliation:
Department of Mathematics, Imperial College London, London, SW7 2AZ, UK (e-mail: [email protected], [email protected], [email protected])
VINCENT P. H. GOVERSE
Affiliation:
Department of Mathematics, Imperial College London, London, SW7 2AZ, UK (e-mail: [email protected], [email protected], [email protected])
JEROEN S. W. LAMB
Affiliation:
Department of Mathematics, Imperial College London, London, SW7 2AZ, UK (e-mail: [email protected], [email protected], [email protected]) International Research Center for Neurointelligence, The University of Tokyo, Tokyo 113-0033, Japan Centre for Applied Mathematics and Bioinformatics, Department of Mathematics and Natural Sciences, Gulf University for Science and Technology, Halwally, Kuwait
MARTIN RASMUSSEN
Affiliation:
Department of Mathematics, Imperial College London, London, SW7 2AZ, UK (e-mail: [email protected], [email protected], [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider absorbing Markov chains $X_n$ admitting a quasi-stationary measure $\mu $ on M where the transition kernel ${\mathcal P}$ admits an eigenfunction 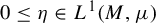$0\leq \eta \in L^1(M,\mu )$. We find conditions on the transition densities of ${\mathcal P}$ with respect to $\mu $ which ensure that $\eta (x) \mu (\mathrm {d} x)$ is a quasi-ergodic measure for 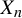$X_n$ and that the Yaglom limit converges to the quasi-stationary measure $\mu $-almost surely. We apply this result to the random logistic map $X_{n+1} = \omega _n X_n (1-X_n)$ absorbed at ${\mathbb R} \setminus [0,1],$ where 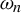$\omega _n$ is an independent and identically distributed sequence of random variables uniformly distributed in $[a,b],$ for $1\leq a <4$ and $b>4.$

Keywords

Markov chains with absorptionrandom dynamical systemsquasi-stationary measurequasi-ergodic measureYaglom limit

MSC classification

Primary: 37H05: Foundations, general theory of cocycles, algebraic ergodic theory 60J05: Discrete-time Markov processes on general state spaces
Secondary: 47B65: Positive operators and order-bounded operators
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 7 , July 2024 , pp. 1818 - 1855
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abbasi, N., Gharaei, M. and Homburg, A. J.. Iterated function systems of logistic maps: synchronization and intermittency. Nonlinearity 31(8) (2018), 3880–3913.CrossRefGoogle Scholar
Athreya, K. B. and Dai, J.. Random logistic maps. I. J. Theoret. Probab. 13(2) (2000), 595–608.CrossRefGoogle Scholar
Benaïm, M., Champagnat, N., Oçafrain, W. and Villemonais, D.. Degenerate processes killed at the boundary of a domain. Preprint, 2021, arXiv:2103.08534.Google Scholar
Breyer, L. A. and Roberts, G. O.. A quasi-ergodic theorem for evanescent processes. Stochastic Process. Appl. 84(2) (1999), 177–186.CrossRefGoogle Scholar
Brezis, H.. Functional Analysis, Sobolev Spaces and Partial Differential Equations (Universitext). Springer, New York, 2011.CrossRefGoogle Scholar
Castro, M. M., Chemnitz, D., Chu, H., Engel, M., Lamb, J. S. W. and Rasmussen, M.. The Lyapunov spectrum for conditioned random dynamical systems. Ann. Henri Poincaré, to appear.Google Scholar
Castro, M. M., Lamb, J. S. W., Olicón-Méndez, G. and Rasmussen, M.. Existence and uniqueness of quasi-stationary and quasi-ergodic measures for absorbing Markov processes: a Banach lattice approach. Preprint, 2022, arXiv:2111.13791.Google Scholar
Champagnat, N. and Villemonais, D.. Exponential convergence to quasi-stationary distribution and Q-process. Probab. Theory Related Fields 164(1–2) (2016), 243–283.CrossRefGoogle Scholar
Darroch, J. N. and Seneta, E.. On quasi-stationary distributions in absorbing discrete-time finite Markov chains. J. Appl. Probab. 2(1) (1965), 88–100.CrossRefGoogle Scholar
Eisner, T., Farkas, B., Haase, M. and Nagel, R.. Operator Theoretic Aspects of Ergodic Theory (Graduate Texts in Mathematics, 272). Springer, Cham, 2015.CrossRefGoogle Scholar
Engel, M., Lamb, J. S. W. and Rasmussen, M.. Conditioned Lyapunov exponents for random dynamical systems. Trans. Amer. Math. Soc. 372(9) (2019), 6343–6370.CrossRefGoogle Scholar
Foguel, S. R.. The Ergodic Theory of Markov Processes (Van Nostrand Mathematical Studies, 21). Van Nostrand Reinhold Co., New York–Toronto, ON–London, 1969.Google Scholar
Folland, G. B.. Real Analysis: Modern Techniques and Their Applications (Pure and Applied Mathematics), 2nd edn. John Wiley & Sons, Inc., New York, 1999; A Wiley-Interscience Publication.Google Scholar
Gerlach, M. and Glück, J.. Convergence of positive operator semigroups. Trans. Amer. Math. Soc. 372(9) (2019), 6603–6627.CrossRefGoogle Scholar
Glück, J.. Aperiodicity of positive operators that increase the support of functions. Preprint, 2022, arXiv:2209.01171.Google Scholar
Glück, J. and Haase, M.. Asymptotics of operator semigroups via the semigroup at infinity. Positivity and Noncommutative Analysis (Trends in Mathematics). Birkhäuser/Springer, Cham, 2019, pp. 167–203.CrossRefGoogle Scholar
Jakobson, M. V.. Absolutely continuous invariant measures for one-parameter families of one-dimensional maps. Comm. Math. Phys. 81(1) (1981), 39–88.CrossRefGoogle Scholar
Krengel, U.. Ergodic Theorems (De Gruyter Studies in Mathematics, 6). Walter de Gruyter, Berlin, 2011.Google Scholar
Lasota, A. and Mackey, M. C.. Chaos, Fractals, and Noise: Stochastic Aspects of Dynamics (Applied Mathematical Sciences, 97). Springer Science & Business Media, New York, 2013.Google Scholar
Lin, M.. On weakly mixing Markov operators and non-singular transformations. Z. Wahrsch. Verwandte Gebiete 55(2) (1981), 231–236.CrossRefGoogle Scholar
Love, E. R.. 64.4 some logarithm inequalities. Math. Gaz. 64(427) (1980), 55–57.CrossRefGoogle Scholar
Meyer-Nieberg, P.. Banach Lattices. Springer Science & Business Media, Berlin–Heidelberg, 2012.Google Scholar
Oçafrain, W., Quasi-stationarity and quasi-ergodicity for discrete-time Markov chains with absorbing boundaries moving periodically. ALEA Lat. Am. J. Probab. Math. Stat. 15(1) (2018), 429–451.CrossRefGoogle Scholar
Oikhberg, T. and Troitsky, V. G.. A theorem of Krein revisited. Rocky Mountain J. Math. 35(1) (2005), 195–210.CrossRefGoogle Scholar
Pflug, G.. Banach lattices and positive operators-H. H. Schaefer. Metrika 23 (1976), 193–193.CrossRefGoogle Scholar
Pollett, P. K.. Quasi-stationary distributions: a bibliography, 2008. Available at https://people.smp.uq.edu.au/PhilipPollett/papers/qsds/qsds.pdf.Google Scholar
Rogers, L. C. G. and Williams, D.. Diffusions, Markov Processes and Martingales, Volume 1: Foundations (Cambridge Mathematical Library, 7). John Wiley & Sons, Ltd., Chichester, 1994.Google Scholar
Viana, M. and Oliveira, K.. Foundations of Ergodic Theory (Cambridge Studies in Advanced Mathematics, 151). Cambridge University Press, Cambridge, 2016.Google Scholar
Zhang, J., Li, S. and Song, R.. Quasi-stationarity and quasi-ergodicity of general Markov processes. Sci. China Math. 57(10) (2014), 2013–2024.CrossRefGoogle Scholar
Zmarrou, H. and Homburg, A. J.. Bifurcations of stationary measures of random diffeomorphisms. Ergod. Th. & Dynam. Sys. 27(5) (2007), 1651–1692.CrossRefGoogle Scholar