Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T04:53:51.575Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of maximizing measures for irreducible countable Markov shifts: a dynamical proof

Published online by Cambridge University Press:  18 March 2013

RODRIGO BISSACOT  and
RICARDO DOS SANTOS FREIRE JR
RODRIGO BISSACOT
Affiliation:
Department of Applied Mathematics, IME-USP, Brazil email [email protected]
RICARDO DOS SANTOS FREIRE JR
Affiliation:
Department of Mathematics, IME-USP, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that if 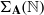${\Sigma }_{\mathbf{A} } ( \mathbb{N} )$ is an irreducible Markov shift space over 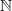$ \mathbb{N} $ and 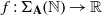$f: {\Sigma }_{\mathbf{A} } ( \mathbb{N} )\rightarrow \mathbb{R} $ is coercive with bounded variation then there exists a maximizing probability measure for 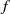$f$, whose support lies on a Markov subshift over a finite alphabet. Furthermore, the support of any maximizing measure is contained in this same compact subshift. To the best of our knowledge, this is the first proof beyond the finitely primitive case in the general irreducible non-compact setting. It is also noteworthy that our technique works for the full shift over positive real sequences.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1103 - 1115
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atkinson, G.. Recurrence of co-cycles and random walks. J. Lond. Math. Soc. 2 (1976), 486–488.Google Scholar
Bissacot, R. and Garibaldi, E.. Weak KAM methods and ergodic optimal problems for countable Markov shifts. Bull. Braz. Math. Soc. 41 (2010), 321–338.Google Scholar
Bousch, T.. La condition de Walters. Ann. Sci. Éc. Norm. Supér. 34 (2001), 287–311.Google Scholar
Iommi, G.. Ergodic optimization for renewal type shifts. Monatsh. Math. 150 (2007), 91–95.CrossRefGoogle Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. Ser. A 15 (2006), 197–224.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Zero temperature limits of Gibbs-equilibrium states for countable alphabet subshifts of finite type. J. Stat. Phys. 119 (2005), 765–776.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Ergodic optimization for countable alphabet subshifts of finite type. Ergod. Th. & Dynam. Sys. 26 (2006), 1791–1803.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Ergodic optimization for non-compact dynamical systems. Dyn. Syst. 22 (2007), 379–388.Google Scholar
Morris, I. D.. Entropy for zero-temperature limits of Gibbs-equilibrium states for countable-alphabet subshifts of finite type. J. Stat. Phys. 126 (2007), 315–324.Google Scholar
Morris, I. D.. A sufficient condition for the subordination principle in ergodic optimization. Bull. Lond. Math. Soc. 39 (2007), 214–220.Google Scholar
Parthasarathy, K. R.. On the category of ergodic measures. Illinois J. Math. 5 (1961), 648–656.Google Scholar