Published online by Cambridge University Press: 17 October 2018
Several perturbation tools are established in the volume-preserving setting allowing for the pasting, extension, localized smoothing and local linearization of vector fields. The pasting and the local linearization hold in all classes of regularity ranging from 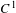 $C^{1}$ to
$C^{1}$ to 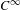 $C^{\infty }$ (Hölder included). For diffeomorphisms, a conservative linearized version of Franks’ lemma is proved in the
$C^{\infty }$ (Hölder included). For diffeomorphisms, a conservative linearized version of Franks’ lemma is proved in the 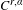 $C^{r,\unicode[STIX]{x1D6FC}}$ (
$C^{r,\unicode[STIX]{x1D6FC}}$ (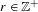 $r\in \mathbb{Z}^{+}$,
$r\in \mathbb{Z}^{+}$, 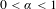 $0<\unicode[STIX]{x1D6FC}<1$) and
$0<\unicode[STIX]{x1D6FC}<1$) and 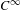 $C^{\infty }$ settings, the resulting diffeomorphism having the same regularity as the original one.
$C^{\infty }$ settings, the resulting diffeomorphism having the same regularity as the original one.