Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T22:09:59.802Z Has data issue: false hasContentIssue false
  • English
  • Français

On self-similar measures with absolutely continuous projections and dimension conservation in each direction

Part of: Classical measure theory

Published online by Cambridge University Press:  26 June 2019

ARIEL RAPAPORT
ARIEL RAPAPORT*
Affiliation:
Centre for Mathematical Sciences, Wilberforce Road, CambridgeCB3 0WA, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

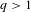Relying on results due to Shmerkin and Solomyak, we show that outside a zero-dimensional set of parameters, for every planar homogeneous self-similar measure $\unicode[STIX]{x1D708}$, with strong separation, dense rotations and dimension greater than $1$, there exists $q>1$ such that 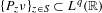$\{P_{z}\unicode[STIX]{x1D708}\}_{z\in S}\subset L^{q}(\mathbb{R})$. Here $S$ is the unit circle and 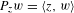$P_{z}w=\langle z,w\rangle$ for 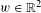$w\in \mathbb{R}^{2}$. We then study such measures. For instance, we show that $\unicode[STIX]{x1D708}$ is dimension conserving in each direction and that the map 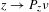$z\rightarrow P_{z}\unicode[STIX]{x1D708}$ is continuous with respect to the weak topology of 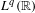$L^{q}(\mathbb{R})$.

Keywords

self-similar sets and measuresabsolute continuitydimension conservation

MSC classification

Primary: 28A80: Fractals
Secondary: 28A78: Hausdorff and packing measures
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 12 , December 2020 , pp. 3438 - 3456
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Einsiedler, M. and Ward, T.. Ergodic Theory with a View towards Number Theory (Graduate Texts in Mathematics, 259). Springer, London, 2011.Google Scholar
Falconer, K.. The Geometry of Fractal Sets. Cambridge University Press, New York, 1985.Google Scholar
Falconer, K.. Techniques in Fractal Geometry. Wiley, Chichester, 1997.Google Scholar
Feng, D.-J. and Hu, H.. Dimension theory of iterated function systems. Comm. Pure Appl. Math. 62 (2009), 1435–1500.Google Scholar
Falconer, K. and Jin, X.. Exact dimensionality and projections of random self-similar measures and sets. J. Lond. Math. Soc. (2) 90(2) (2014), 388–412.Google Scholar
Falconer, K. and Jin, X.. Dimension conservation for self-similar sets and fractal percolation. Int. Math. Res. Not. IMRN 2015(24) (2015), 13260–13289.Google Scholar
Fan, A.-H., Lau, K.-S. and Rao, H.. Relationships between different dimensions of a measure. Monatsh. Math. 135 (2002), 191–201.Google Scholar
Folland, G.. Real Analysis: Modern Techniques and Their Applications (Pure Applied Mathematics), 2nd edn. Wiley, New York, 1999.Google Scholar
Furstenberg, H.. Ergodic fractal measures and dimension conservation. Ergod. Th. & Dynam. Sys. 28 (2008), 405–422.Google Scholar
Hunt, B. and Kaloshin, V.. How projections affect the dimension spectrum of fractal measures. Nonlinearity 10 (1997), 1031–1046.Google Scholar
Hochman, M. and Shmerkin, P.. Local entropy averages and projections of fractal measures. Ann. of Math. (2) 175(3) (2012), 1001–1059.Google Scholar
Järvenpää, M. and Mattila, P.. Hausdorff and packing dimensions and sections of measures. Mathematika 45 (1998), 55–77.Google Scholar
Mattila, P.. Geometry of sets and measures in euclidean spaces. Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics, 44). Cambridge University Press, Cambridge, 1995.Google Scholar
Mauldin, D. and Simon, K.. The equivalence of some Bernoulli convolutions to Lebesgue measure. Proc. Amer. Math. Soc. 126(9) (1998), 2733–2736.Google Scholar
Peres, Y. and Shmerkin, P.. Resonance between cantor sets. Ergod. Th. & Dynam. Sys. 29 (2009), 201–221.Google Scholar
Peres, Y., Schlag, W. and Solomyak, B.. Sixty years of Bernoulli convolutions. Fractal Geometry and Stochastics II. Eds. Bandt, C., Graf, S. and Zähle, BM.. Birkhäuser, Basel, 2000, pp. 39–65.Google Scholar
Rapaport, A.. On the Hausdorff and packing measures of slices of dynamically defined sets. J. Frac. Geom. 3(1) (2016), 33–74.Google Scholar
Rapaport, A.. A self-similar measure with dense rotations, singular projections and discrete slices. Adv. Math. 321 (2017), 529–546.Google Scholar
Shmerkin, P.. On the exceptional set for absolute continuity of Bernoulli convolutions. Geom. Funct. Anal. 24(3) (2014), 946–958.Google Scholar
Shmerkin, P.. On Furstenberg’s intersection conjecture, self-similar measures, and the $L^{q}$ norms of convolutions. Preprint, 2016, arXiv:609.07802.Google Scholar
Shmerkin, P. and Solomyak, B.. Absolute continuity of self-similar measures, their projections and convolutions. Trans. Amer. Math. Soc. 368(7) (2016), 5125–5151.Google Scholar
Shmerkin, P. and Solomyak, B.. Absolute continuity of complex Bernoulli convolutions. Math. Proc. Cambridge Philos. Soc. 161(3) (2016), 435–453.Google Scholar