Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shinoda, Mao
2018.
Uncountably many maximizing measures for a dense subset of continuous functions.
Nonlinearity,
Vol. 31,
Issue. 5,
p.
2192.
Basurto, Eduardo
Haro-Pérez, Catalina
Vargas, Carlos A.
and
Odriozola, Gerardo
2018.
Massive replica exchange Monte Carlo algorithm: a tool to access high pressure thermodynamics of hard systems.
Physical Chemistry Chemical Physics,
Vol. 20,
Issue. 43,
p.
27490.
Catsigeras, Eleonora
and
Troubetzkoy, Serge
2019.
Invariant measures for typical continuous maps on manifolds.
Nonlinearity,
Vol. 32,
Issue. 10,
p.
3981.
Díaz, L. J.
Gelfert, K.
and
Rams, M.
2019.
Entropy Spectrum of Lyapunov Exponents for Nonhyperbolic Step Skew-Products and Elliptic Cocycles.
Communications in Mathematical Physics,
Vol. 367,
Issue. 2,
p.
351.
Díaz, L. J.
Gelfert, K.
Marcarini, T.
and
Rams, M.
2019.
The structure of the space of ergodic measures of transitive partially hyperbolic sets.
Monatshefte für Mathematik,
Vol. 190,
Issue. 3,
p.
441.
Menceur, Mohamed
and
Mabrouk, Anouar Ben
2019.
A joint multifractal analysis of vector valued non Gibbs measures.
Chaos, Solitons & Fractals,
Vol. 126,
Issue. ,
p.
203.
Airey, Dylan
Jackson, Steve
Kwietniak, Dominik
and
Mance, Bill
2020.
Borel complexity of sets of normal numbers via generic points in subshifts with specification.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 7,
p.
4561.
Osipenko, Georgy Sergeevich
2020.
Кодировка траекторий и инвариантных мер.
Математический сборник,
Vol. 211,
Issue. 7,
p.
151.
Takahasi, Hiroki
2020.
Entropy-approachability for transitive Markov shifts over infinite alphabet.
Proceedings of the American Mathematical Society,
Vol. 148,
Issue. 9,
p.
3847.
Osipenko, G. S.
2020.
Encodings of trajectories and invariant measures.
Sbornik: Mathematics,
Vol. 211,
Issue. 7,
p.
1041.
Selmi, Bilel
2020.
On the effect of projections on the Billingsley dimensions.
Asian-European Journal of Mathematics,
Vol. 13,
Issue. 07,
p.
2050128.
BURR, MICHAEL A.
SCHMOLL, MARTIN
and
WOLF, CHRISTIAN
2020.
On the computability of rotation sets and their entropies.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 2,
p.
367.
Carvalho, Silas L.
and
Condori, Alexander
2021.
Generic properties of invariant measures of full-shift systems over perfect Polish metric spaces.
Stochastics and Dynamics,
Vol. 21,
Issue. 07,
Carvalho, Silas L.
and
Condori, Alexander
2021.
Generalized fractal dimensions of invariant measures of full-shift systems over compact and perfect spaces: generic behavior.
Forum Mathematicum ,
Vol. 33,
Issue. 2,
p.
435.
Berger, Pierre
and
Bochi, Jairo
2021.
On emergence and complexity of ergodic decompositions.
Advances in Mathematics,
Vol. 390,
Issue. ,
p.
107904.
PAVEZ-MOLINA, SEBASTIÁN
2022.
Generic rotation sets.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 1,
p.
250.
He, Yan Mary
and
Wolf, Christian
2022.
Entropy spectrum of rotation classes.
Journal of Mathematical Analysis and Applications,
Vol. 508,
Issue. 1,
p.
125851.
Pacifico, Maria José
and
Sanhueza, Diego
2022.
On Bowen's entropy inequality and almost specification for flows.
Journal of Differential Equations,
Vol. 335,
Issue. ,
p.
43.
Gorodetski, Anton
and
Luna, Alexandro
2023.
Thomae's function and the space of ergodic measures.
Dynamical Systems,
Vol. 38,
Issue. 2,
p.
268.
Jacelon, Bhishan
2023.
Chaotic tracial dynamics.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
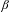 $\unicode[STIX]{x1D6FD}$-shifts and
$\unicode[STIX]{x1D6FD}$-shifts and  $S$-gap shifts,
$S$-gap shifts, 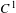 $C^{1}$-generic diffeomorphisms of a compact manifold
$C^{1}$-generic diffeomorphisms of a compact manifold 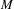 $M$ and certain geodesic flows of a complete connected negatively curved manifold.
$M$ and certain geodesic flows of a complete connected negatively curved manifold.

