Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T06:33:35.368Z Has data issue: false hasContentIssue false
  • English
  • Français

The numbers of periodic orbits hidden at fixed points of holomorphic maps

Part of: Complex dynamical systems Holomorphic mappings and correspondences Smooth dynamical systems: general theory

Published online by Cambridge University Press:  03 September 2019

JIANYONG QIAO ,
HONGYU QU  and
GUANGYUAN ZHANG
JIANYONG QIAO
Affiliation:
School of Sciences, Beijing University of Posts and Telecommunications, Beijing100786, PR China email [email protected]
HONGYU QU
Affiliation:
School of Computer Science, Beijing University of Posts and Telecommunications, Beijing100786, PR China email [email protected]
GUANGYUAN ZHANG
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing100084, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 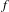$f$ be an $n$-dimensional holomorphic map defined in a neighborhood of the origin such that the origin is an isolated fixed point of all of its iterates, and let 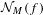${\mathcal{N}}_{M}(f)$ denote the number of periodic orbits of 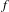$f$ of period 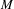$M$ hidden at the origin. Gorbovickis gives an efficient way of computing 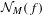${\mathcal{N}}_{M}(f)$ for a large class of holomorphic maps. Inspired by Gorbovickis’ work, we establish a similar method for computing 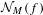${\mathcal{N}}_{M}(f)$ for a much larger class of holomorphic germs, in particular, having arbitrary Jordan matrices as their linear parts. Moreover, we also give another proof of the result of Gorbovickis [On multi-dimensional Fatou bifurcation. Bull. Sci. Math.138(3)(2014) 356–375] using our method.

Keywords

smooth dynamicsperiodic orbitsholomorphic mapsfixed-point indicesDold indices

MSC classification

Primary: 32H50: Iteration problems 37C25: Fixed points, periodic points, fixed-point index theory
Secondary: 37F45: Holomorphic families of dynamical systems; the Mandelbrot set; bifurcations 37F50: Small divisors, rotation domains and linearization; Fatou and Julia sets
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 2 , February 2021 , pp. 578 - 592
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, V. I., Gusein-Zade, S. M. and Varchenko, A. N.. Singularities of Differentiable Maps. Vol. I: The Classification of Critical Points Caustics and Wave Fronts. Birkhäuser, Boston, MA, 1985.CrossRefGoogle Scholar
Dold, A.. Fixed point indices of iterated maps. Invent. Math. 74.3(1983) 419–435.Google Scholar
Gorbovickis, I.. On multi-dimensional Fatou bifurcation. Bull. Sci. Math. 138.3(2014) 356–375.Google Scholar
Lloyd, N. G.. Degree Theory (Cambridge Tracts in Mathematics, 73) . Cambridge University Press, Cambridge, 1978.Google Scholar
Shub, M. and Sullivan, D.. A remark on the Lefschetz fixed point formula for differentiable maps. Topology 13(1974) 189–191.CrossRefGoogle Scholar
Yang, Z. M.. Probability Theory. Science Press, Beijing, 1999, pp. 31–32 (in Chinese).Google Scholar
Zhang, G. Y.. Bifurcations of periodic points of holomorphic maps from ℂ2 into ℂ2 . Proc. Lond. Math. Soc. (3) 79(3) (1999), 353–380.CrossRefGoogle Scholar
Zhang, G. Y.. Fixed point indices and periodic points of holomorphic mappings. Math. Ann. 337(2) (2007), 401–433.CrossRefGoogle Scholar
Zhang, G. Y.. The numbers of periodic orbits hidden at fixed points of n-dimensional holomorphic mappings(II). Topol. Methods Nonlinear Anal. 33(1) (2009), 65–83.CrossRefGoogle Scholar