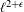Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T05:45:17.373Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-uniqueness for specifications in $\ell ^{2+\unicode[STIX]{x1D716}}$

Published online by Cambridge University Press:  20 March 2017

NOAM BERGER ,
CHRISTOPHER HOFFMAN  and
VLADAS SIDORAVICIUS
NOAM BERGER
Affiliation:
Department of Mathematics, Technische Universität München, Boltzmannstrasse 3, 85748 Garching, Germany Department of Mathematics, the Hebrew University of Jerusalem, Israel
CHRISTOPHER HOFFMAN
Affiliation:
Department of Mathematics, Box #354350, University of Washington, Seattle, WA 98195-4350, USA
VLADAS SIDORAVICIUS
Affiliation:
Courant Institute of Mathematical Sciences, NYU, New York, USA NYU-ECNU Institute of Mathematical Sciences at NYU Shanghai, Shanghai, China Cemaden, São José dos Campos, Brasil
Get access Rights & Permissions [Opens in a new window]

Abstract

For every 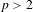$p>2$, we construct a regular and continuous specification ($g$-function), which has a variation sequence that is in 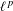$\ell ^{p}$ and which admits multiple Gibbs measures. Combined with a result of Johansson and Öberg [Square summability of variations of $g$-functions and uniqueness in $g$-measures. Math. Res. Lett.10(5–6) (2003), 587–601], this determines the optimal modulus of continuity for a specification which admits multiple Gibbs measures.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 4 , June 2018 , pp. 1342 - 1352
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aizenman, M., Chayes, J. T., Chayes, L. and Newman, C. M.. Discontinuity of the magnetization in one-dimensional 1/|x - y|2 Ising and Potts models. J. Stat. Phys. 50(1–2) (1988), 1–40.Google Scholar
Aizenman, M. and Newman, C. M.. Discontinuity of the percolation density in one-dimensional 1/|x - y|2 percolation models. Comm. Math. Phys. 107(4) (1986), 611–647.Google Scholar
Berbee, H.. Chains with infinite connections: uniqueness and Markov representation. Probab. Theory Related Fields 76 (1987), 243–253.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Springer, Berlin, 1975.Google Scholar
Bramson, M. and Kalikow, S.. Nonuniqueness in g-functions. Israel J. Math. 84 (1993), 153–160.Google Scholar
Dias, J. and Friedli, S.. Uniqueness vs non-uniqueness in complete connections with modified majority rules. Probab. Theory Related Fields 164(3) (2016), 893–929.Google Scholar
Döblin, W. and Fortet, R.. Sur des chaines a liaisons completès. Bull. Soc. Math. France 65 (1937), 132–148.Google Scholar
Dyson, F.. Existence of a phase-transition in a one-dimensional Ising ferromagnet. Comm. Math. Phys. 12(2) (1969), 91–107.CrossRefGoogle Scholar
Fernández, R. and Maillard, G.. Chains with complete connections and one-dimensional Gibbs measures. Electron. J. Probab. 9(6) (2004), 145–176.Google Scholar
Fernández, R. and Maillard, G.. Chains with complete connections: general theory, uniqueness, loss of memory and mixing properties. J. Stat. Phys. 118(3–4) (2005), 555–588.Google Scholar
Fröhlich, J. and Spencer, T.. The phase transition in the one-dimensional Ising model with 1/r 2 interaction energy. Comm. Math. Phys. 84(1) (1982), 87–101.CrossRefGoogle Scholar
Harris, T.. On chains of infinite order. Pacific J. Math. 5 (1955), 707–724.CrossRefGoogle Scholar
Hulse, P.. An example of non-unique g-measures. Ergod. Th. & Dynam. Sys. 26(2) (2006), 439–445.Google Scholar
Johansson, A. and Öberg, A.. Square summability of variations of g-functions and uniqueness in g-measures. Math. Res. Lett. 10(5–6) (2003), 587–601.CrossRefGoogle Scholar
Keane, M.. Strongly mixing g-measures. Invent. Math. 16 (1972), 309–324.CrossRefGoogle Scholar
Lalley, S. P.. Regenerative representation for one-dimensional Gibbs states. Ann. Probab. 14 (1986), 1262–1271.CrossRefGoogle Scholar
Ledrappier, F.. Principe variationnel et systèmes dynamiques symboliques. Z. Wahrscheinlichkeitstheorie verw. Geb. 30 (1974), 185–202.Google Scholar
Newman, C. M. and Schulman, L. S.. One-dimensional 1/|j - i| s percolation models: the existence of a transition for s ≤ 2. Comm. Math. Phys. 104(4) (1986), 547–571.CrossRefGoogle Scholar
Ruelle, D.. Statistical mechanics of one-dimensional lattice gas. Comm. Math. Phys. 9 (1968), 267–278.Google Scholar
Sinai, Y. G.. Gibbs measures in ergodic theory. Uspekhi Mat. Nauk 27 (1972), 21–64.Google Scholar
Stenflo, Ö.. Uniqueness of invariant measures for place-dependent random iterations of functions. Fractals in Multimedia (Minneapolis, MN, 2001) (IMA Volumes in Mathematics and its Applications, 132) . Springer, New York, 2002, pp. 13–32.Google Scholar
Stenflo, Ö.. Uniqueness in g-measures. Nonlinearity 16 (2003), 403–410.Google Scholar
Walters, P.. Ruelle’s operator theorem and g-measures. Trans. Amer. Math. Soc. 214 (1975), 375–387.Google Scholar