No CrossRef data available.
Article contents
Non-realizability of the pure braid group as area-preserving homeomorphisms
Published online by Cambridge University Press: 11 June 2020
Abstract
Let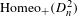 
$\operatorname{Homeo}_{+}(D_{n}^{2})$ be the group of orientation-preserving homeomorphisms of 
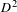$D^{2}$ fixing the boundary pointwise and 
$n$ marked points as a set. The Nielsen realization problem for the braid group asks whether the natural projection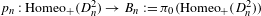 
$p_{n}:\operatorname{Homeo}_{+}(D_{n}^{2})\rightarrow B_{n}:=\unicode[STIX]{x1D70B}_{0}(\operatorname{Homeo}_{+}(D_{n}^{2}))$ has a section over subgroups of 
$B_{n}$. All of the previous methods use either torsion or Thurston stability, which do not apply to the pure braid group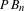 
$PB_{n}$, the subgroup of 
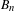$B_{n}$ that fixes 
$n$ marked points pointwise. In this paper, we show that the pure braid group has no realization inside the area-preserving homeomorphisms using rotation numbers.
- Type
- Original Article
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press
References
Chen, L.. On the nonrealizability of braid groups by homeomorphisms. Geom. Topol.
23(7) (2019), 3735–3749.10.2140/gt.2019.23.3735CrossRefGoogle Scholar
Chen, L. and Markovic, V.. Non-realizability of the Torelli group as area-preserving homeomorphisms. J. Lond. Math. Soc., accepted. Preprint, 2019, arXiv:1904.09490.Google Scholar
Farb, B. and Margalit, D.. A Primer on Mapping Class Groups
(Princeton Mathematical Series, 49)
. Princeton University Press, Princeton, NJ, 2012.Google Scholar
Franks, J.. Rotation numbers and instability sets. Bull. Amer. Math. Soc. (N.S.)
40(3) (2003), 263–279.10.1090/S0273-0979-03-00983-2CrossRefGoogle Scholar
Franks, J. and Le Calvez, P.. Regions of instability for non-twist maps. Ergod. Th. & Dynam. Sys.
23(1) (2003), 111–141.10.1017/S0143385702000858CrossRefGoogle Scholar
Handel, M.. The rotation set of a homeomorphism of the annulus is closed. Comm. Math. Phys.
127(2) (1990), 339–349.10.1007/BF02096762CrossRefGoogle Scholar
Hubbard, J.. Teichmüller Theory and Applications to Geometry, Topology, and Dynamics. Vol. 1. Matrix Editions, Ithaca, NY, 2006, Teichmüller theory, with contributions by A. Douady, W. Dunbar, R. Roeder, S. Bonnot, D. Brown, A. Hatcher, C. Hruska and S. Mitra, with forewords by W. Thurston and C. Earle.Google Scholar
Mann, K. and Tshishiku, B.. Realization problems for diffeomorphism groups. Proc. Georgia International Topology Festival, accepted. Preprint, 2018, arXiv:1802.00490.Google Scholar
Markovic, V.. Realization of the mapping class group by homeomorphisms. Invent. Math.
168(3) (2007), 523–566.CrossRefGoogle Scholar
Matsumoto, S.. Prime end rotation numbers of invariant separating continua of annular homeomorphisms. Proc. Amer. Math. Soc.
140(3) (2012), 839–845.10.1090/S0002-9939-2011-11435-7CrossRefGoogle Scholar
Milnor, J.. Dynamics in One Complex Variable
(Annals of Mathematics Studies, 160)
, 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Salter, N. and Tshishiku, B.. On the non-realizability of braid groups by diffeomorphisms. Bull. Lond. Math. Soc.
48(3) (2016), 457–471.10.1112/blms/bdw016CrossRefGoogle Scholar