No CrossRef data available.
Article contents
A new mean ergodic theorem for tori and recurrences
Published online by Cambridge University Press: 07 October 2019
Abstract
Let 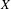 $X$ be a finite-dimensional connected compact abelian group equipped with the normalized Haar measure
$X$ be a finite-dimensional connected compact abelian group equipped with the normalized Haar measure  $\unicode[STIX]{x1D707}$. We obtain the following mean ergodic theorem over ‘thin’ phase sets. Fix
$\unicode[STIX]{x1D707}$. We obtain the following mean ergodic theorem over ‘thin’ phase sets. Fix 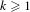 $k\geq 1$ and, for every
$k\geq 1$ and, for every 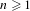 $n\geq 1$, let
$n\geq 1$, let 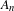 $A_{n}$ be a subset of
$A_{n}$ be a subset of 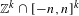 $\mathbb{Z}^{k}\cap [-n,n]^{k}$. Assume that
$\mathbb{Z}^{k}\cap [-n,n]^{k}$. Assume that 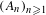 $(A_{n})_{n\geq 1}$ has
$(A_{n})_{n\geq 1}$ has 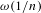 $\unicode[STIX]{x1D714}(1/n)$ density in the sense that
$\unicode[STIX]{x1D714}(1/n)$ density in the sense that 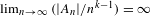 $\lim _{n\rightarrow \infty }(|A_{n}|/n^{k-1})=\infty$. Let
$\lim _{n\rightarrow \infty }(|A_{n}|/n^{k-1})=\infty$. Let  $T_{1},\ldots ,T_{k}$ be ergodic automorphisms of
$T_{1},\ldots ,T_{k}$ be ergodic automorphisms of 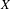 $X$. We have
$X$. We have  $$\begin{eqnarray}\frac{1}{|A_{n}|}\mathop{\sum }_{(n_{1},\ldots ,n_{k})\in A_{n}}f_{1}(T_{1}^{n_{1}}(x))\cdots f_{k}(T_{k}^{n_{k}}(x))\stackrel{L_{\unicode[STIX]{x1D707}}^{2}}{\longrightarrow }\int f_{1}\,d\unicode[STIX]{x1D707}\cdots \int f_{k}\,d\unicode[STIX]{x1D707},\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{|A_{n}|}\mathop{\sum }_{(n_{1},\ldots ,n_{k})\in A_{n}}f_{1}(T_{1}^{n_{1}}(x))\cdots f_{k}(T_{k}^{n_{k}}(x))\stackrel{L_{\unicode[STIX]{x1D707}}^{2}}{\longrightarrow }\int f_{1}\,d\unicode[STIX]{x1D707}\cdots \int f_{k}\,d\unicode[STIX]{x1D707},\end{eqnarray}$$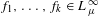 $f_{1},\ldots ,f_{k}\in L_{\unicode[STIX]{x1D707}}^{\infty }$. When the
$f_{1},\ldots ,f_{k}\in L_{\unicode[STIX]{x1D707}}^{\infty }$. When the 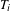 $T_{i}$ are ergodic epimorphisms, the same conclusion holds under the further assumption that
$T_{i}$ are ergodic epimorphisms, the same conclusion holds under the further assumption that 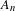 $A_{n}$ is a subset of
$A_{n}$ is a subset of 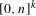 $[0,n]^{k}$ for every
$[0,n]^{k}$ for every  $n$. The density assumption on the
$n$. The density assumption on the 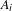 $A_{i}$ is necessary. Immediate applications include certain Poincaré style recurrence results.
$A_{i}$ is necessary. Immediate applications include certain Poincaré style recurrence results.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019



