Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T10:14:36.769Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicity of topological systems

Part of: Ergodic theory

Published online by Cambridge University Press:  05 February 2024

DAVID BURGUET  and
RUXI SHI
DAVID BURGUET*
Affiliation:
Sorbonne Universite, LPSM, 75005 Paris, France (e-mail: [email protected])
RUXI SHI
Affiliation:
Sorbonne Universite, LPSM, 75005 Paris, France (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define the topological multiplicity of an invertible topological system 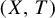$(X,T)$ as the minimal number k of real continuous functions $f_1,\ldots , f_k$ such that the functions 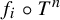$f_i\circ T^n$, 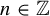$n\in {\mathbb {Z}}$, 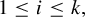$1\leq i\leq k,$ span a dense linear vector space in the space of real continuous functions on X endowed with the supremum norm. We study some properties of topological systems with finite multiplicity. After giving some examples, we investigate the multiplicity of subshifts with linear growth complexity.

Keywords

topological multiplicitytopological dynamicstopological rankentropyergodic theory

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 10 , October 2024 , pp. 2832 - 2858
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Atzmon, A. and Olevskiĭ, A.. Completeness of integer translates in function spaces on R. J. Approx. Theory 87(3) (1996), 291–327.10.1006/jath.1996.0106CrossRefGoogle Scholar
Baxter, J. R.. A class of ergodic transformations having simple spectrum. Proc. Amer. Math. Soc. 27 (1971), 275–279.10.1090/S0002-9939-1971-0276440-2CrossRefGoogle Scholar
Birkhoff, G. D.. Demonstration d’un theoreme elementaire sur les fonctions entieres. C. R. Math. Acad. Sci. Paris 189 (1929), 473–475.Google Scholar
Boshernitzan, M.. A unique ergodicity of minimal symbolic flows with linear block growth. J. Anal. Math. 44(1) (1984), 77–96.10.1007/BF02790191CrossRefGoogle Scholar
Boshernitzan, M. D.. A condition for unique ergodicity of minimal symbolic flows. Ergod. Th. & Dynam. Sys. 12(3) (1992), 425–428.10.1017/S0143385700006866CrossRefGoogle Scholar
Bourdon, P. S. and Shapiro, J. H.. Cyclic phenomena for composition operators. Mem. Amer. Math. Soc. 125(596) (1997), x+105.Google Scholar
Burguet, D. and Shi, R.. Topological mean dimension of induced systems. Preprint, 2022, arXiv:2206.10508.Google Scholar
Cyr, V. and Kra, B.. Counting generic measures for a subshift of linear growth. J. Eur. Math. Soc. (JEMS) 21(2) (2019), 355–380.10.4171/jems/838CrossRefGoogle Scholar
Coornaert, M.. Topological Dimension and Dynamical Systems. Springer, Cham, 2015.10.1007/978-3-319-19794-4CrossRefGoogle Scholar
Creutz, D. and Pavlov, R.. Low complexity subshifts have discrete spectrum. Forum Math. Sigma 11 (2023), e96.10.1017/fms.2023.95CrossRefGoogle Scholar
Creutz, D.. Measure-theoretically mixing subshifts of minimal word complexity. Preprint, 2023, arXiv:2206.10047.Google Scholar
Danilenko, A. I.. A survey on spectral multiplicities of ergodic actions. Ergod. Th. & Dynam. Sys. 33(1) (2013), 81–117.10.1017/S0143385711000800CrossRefGoogle Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. Interplay between finite topological rank minimal cantor systems, s-adic subshifts and their complexity. Trans. Amer. Math. Soc. 374(5) (2021), 3453–3489.10.1090/tran/8315CrossRefGoogle Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer, Berlin, 2006.Google Scholar
Durand, F. and Perrin, D.. Dimension Groups and Dynamical Systems—Substitutions, Bratteli Diagrams and Cantor Systems (Cambridge Studies in Advanced Mathematics, 196). Cambridge University Press, Cambridge, 2022.10.1017/9781108976039CrossRefGoogle Scholar
Espinoza, B.. The structure of low complexity subshifts. Preprint, 2023, arXiv:2305.03096.Google Scholar
Pytheas Fogg, N.. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794). Eds. V. Berthé, S. Ferenczi, C. Mauduit and A. Siegel. Springer-Verlag, Berlin, 2002.10.1007/b13861CrossRefGoogle Scholar
Gutman, Y. and Tsukamoto, M.. Embedding minimal dynamical systems into Hilbert cubes. Invent. Math. 221(1) (2020), 113–166.10.1007/s00222-019-00942-wCrossRefGoogle Scholar
Glasner, E. and Weiss, B.. Quasi-factors of zero-entropy systems. J. Amer. Math. Soc. 8(3) (1995), 665–686.Google Scholar
Javaheri, M.. Cyclic composition operators on separable locally compact metric spaces. Topology Appl. 258 (2019), 126–141.10.1016/j.topol.2019.03.001CrossRefGoogle Scholar
Kakutani, S.. Strictly ergodic symbolic dynamical systems. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability (Univ. California, Berkeley, CA, 1970/1971), Vol. II: Probability Theory. University of California Press, Berkeley, CA, 1972.Google Scholar
Katok, A.. Cocycles, cohomology and combinatorial constructions in ergodic theory. Smooth Ergodic Theory and its Applications (Seattle, WA, 1999) (Proceedings of Symposia in Pure Mathematics, 69). American Mathematical Society, Providence, RI, 2001, pp. 107–173; in collaboration with E. A. Robinson, Jr.10.1090/pspum/069/1858535CrossRefGoogle Scholar
Kwiatkowski, J. and Lacroix, Y.. Multiplicity, rank pairs. J. Anal. Math. 71 (1997), 205–235.10.1007/BF02788031CrossRefGoogle Scholar
Kwiatkowski, J.. Spectral isomorphism of Morse dynamical systems. Bull. Acad. Polon. Sci. Sér. Sci. Math. 29(3–4) (1981), 105–114.Google Scholar
Lindenstrauss, E.. Mean dimension, small entropy factors and an embedding theorem. Publ. Math. Inst. Hautes Études Sci. 89(1) (1999), 227–262.10.1007/BF02698858CrossRefGoogle Scholar
Lindenstrauss, E. and Tsukamoto, M.. Mean dimension and an embedding problem: an example. Israel J. Math. 199(2) (2014), 573–584.10.1007/s11856-013-0040-9CrossRefGoogle Scholar
Liardet, P. and Voln, D.. Sums of continuous and differentiable functions in dynamical systems. Israel J. Math. 98 (1997), 29–60.10.1007/BF02937328CrossRefGoogle Scholar
Michel, P.. Stricte ergodicité d’ensembles minimaux de substitution. Théorie Ergodique. Eds. Conze, J. P. and Keane, M. S.. Springer, Berlin, 1976, pp. 189–201.10.1007/BFb0080180CrossRefGoogle Scholar
Newton, D. and Parry, W.. On a factor automorphism of a normal dynamical system. Ann. Math. Statist. 37 (1966), 1528–1533.10.1214/aoms/1177699144CrossRefGoogle Scholar
Parasyuk, O. S.. Flows of horocycles on surfaces of constant negative curvature. Uspekhi Mat. Nauk (N.S.) 8(3(55)) (1953), 125–126.Google Scholar
Queffélec, M.. Substitution Dynamical Systems-Spectral Analysis (Lecture Notes in Mathematics, 1294). Springer, Berlin, 2010.10.1007/978-3-642-11212-6CrossRefGoogle Scholar