Article contents
A metric minimal PI cascade with 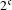 $2^{\mathfrak{c}}$ minimal ideals
$2^{\mathfrak{c}}$ minimal ideals
Published online by Cambridge University Press: 14 September 2018
Abstract
We first improve an old result of McMahon and show that a metric minimal flow whose enveloping semigroup contains less than  $2^{\mathfrak{c}}$ (where
$2^{\mathfrak{c}}$ (where  $\mathfrak{c}=2^{\aleph _{0}}$) minimal left ideals is proximal isometric (PI). Then we show the existence of various minimal PI-flows with many minimal left ideals, as follows. For the acting group
$\mathfrak{c}=2^{\aleph _{0}}$) minimal left ideals is proximal isometric (PI). Then we show the existence of various minimal PI-flows with many minimal left ideals, as follows. For the acting group 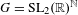 $G=\text{SL}_{2}(\mathbb{R})^{\mathbb{N}}$, we construct a metric minimal PI
$G=\text{SL}_{2}(\mathbb{R})^{\mathbb{N}}$, we construct a metric minimal PI 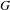 $G$-flow with
$G$-flow with  $\mathfrak{c}$ minimal left ideals. We then use this example and results established in Glasner and Weiss. [On the construction of minimal skew-products. Israel J. Math.34 (1979), 321–336] to construct a metric minimal PI cascade
$\mathfrak{c}$ minimal left ideals. We then use this example and results established in Glasner and Weiss. [On the construction of minimal skew-products. Israel J. Math.34 (1979), 321–336] to construct a metric minimal PI cascade  $(X,T)$ with
$(X,T)$ with  $\mathfrak{c}$ minimal left ideals. We go on to construct an example of a minimal PI-flow
$\mathfrak{c}$ minimal left ideals. We go on to construct an example of a minimal PI-flow 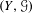 $(Y,{\mathcal{G}})$ on a compact manifold
$(Y,{\mathcal{G}})$ on a compact manifold  $Y$ and a suitable path-wise connected group
$Y$ and a suitable path-wise connected group 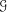 ${\mathcal{G}}$ of a homeomorphism of
${\mathcal{G}}$ of a homeomorphism of  $Y$, such that the flow
$Y$, such that the flow 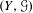 $(Y,{\mathcal{G}})$ is PI and has
$(Y,{\mathcal{G}})$ is PI and has 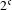 $2^{\mathfrak{c}}$ minimal left ideals. Finally, we use this latter example and a theorem of Dirbák to construct a cascade
$2^{\mathfrak{c}}$ minimal left ideals. Finally, we use this latter example and a theorem of Dirbák to construct a cascade 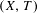 $(X,T)$ that is PI (of order three) and has
$(X,T)$ that is PI (of order three) and has 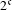 $2^{\mathfrak{c}}$ minimal left ideals. Thus this final result shows that, even for cascades, the converse of the implication ‘less than
$2^{\mathfrak{c}}$ minimal left ideals. Thus this final result shows that, even for cascades, the converse of the implication ‘less than 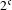 $2^{\mathfrak{c}}$ minimal left ideals implies PI’, fails.
$2^{\mathfrak{c}}$ minimal left ideals implies PI’, fails.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
- 2
- Cited by


