Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-07T07:45:18.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Markov partitions and homology for 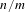$n/m$-solenoids

Published online by Cambridge University Press:  27 November 2015

NIGEL D. BURKE  and
IAN F. PUTNAM
NIGEL D. BURKE
Affiliation:
Department of Pure Mathematics, Cambridge University, Cambridge, CB3 OWB, UK email [email protected]
IAN F. PUTNAM
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Victoria, BC, CanadaV8W 2Y2 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a relatively prime pair of integers, 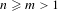$n\geq m>1$, there is associated a topological dynamical system which we refer to as an 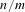$n/m$-solenoid. It is also a Smale space, as defined by David Ruelle, meaning that it has local coordinates of contracting and expanding directions. In this case, these are locally products of the real and various 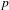$p$-adic numbers. In the special case, 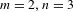$m=2,n=3$ and for 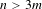$n>3m$, we construct Markov partitions for such systems. The second author has developed a homology theory for Smale spaces and we compute this in these examples, using the given Markov partitions, for all values of 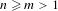$n\geq m>1$ and relatively prime.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 3 , May 2017 , pp. 716 - 738
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amini, M., Gholikandi, S. and Putnam, I. F.. Homology for one-dimensional solenoids. Preprint.Google Scholar
Bowen, R.. Markov partitions for Axiom A diffeomorphisms. Amer. J. Math. 92 (1970), 725–747.Google Scholar
Bowen, R.. On Axiom A Diffeomorphisms (AMS-CBMS Regional Conference, 135) . American Mathematical Society, Providence, RI, 1978.Google Scholar
Gouvea, F. Q.. p-adic Numbers: An Introduction, 2nd edn. Springer, New York, 1997.CrossRefGoogle Scholar
Krieger, W.. On dimension functions and topological Markov chains. Invent. Math. 56 (1980), 239–250.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Putnam, I. F.. A homology theory for Smale spaces. Mem. Amer. Math. Soc., to appear.Google Scholar
Ruelle, D.. Thermodynamic Formalism (Encyclopedia of Mathematics and its Applications, 5) . Addison-Wesley, Reading, MA, 1978.Google Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.Google Scholar
Thomsen, K.. The homoclinic and heteroclinic C ∗ -algebra of a generalized one-dimensional solenoid. Ergod. Th. & Dynam. Sys. 30 (2010), 263–308.CrossRefGoogle Scholar
Ward, T. and Yamama, Y.. Markov partitions reflecting the geometry of × 2 × 3. Discrete Contin. Dyn. Syst. 24(2) (2009), 613–624.Google Scholar
Weiss, B.. The isomorphism problem in ergodic theory. Bull. Amer. Math. Soc. 78 (1972), 668–684.Google Scholar
Williams, R. F.. One-dimensional non-wandering sets. Topology 6 (1967), 37–487.Google Scholar
Wilson, A. M.. On endomorphisms of a solenoid. Proc. Amer. Math. Soc. 55 (1976), 69–74.Google Scholar
Yi, I.. Canonical symbolic dynamics for one-dimensional generalized solenoids. Trans. Amer. Math. Soc. 353 (2001), 3741–3767.Google Scholar