Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T10:43:53.873Z Has data issue: false hasContentIssue false
  • English
  • Français

Lyapunov optimization for non-generic one-dimensional expanding Markov maps

Part of: Ergodic theory Low-dimensional dynamical systems Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  25 March 2019

MAO SHINODA  and
HIROKI TAKAHASI
MAO SHINODA
Affiliation:
Department of Mathematics, Keio University, Yokohama, 223-8522, Japan email [email protected], [email protected]
HIROKI TAKAHASI
Affiliation:
Department of Mathematics, Keio University, Yokohama, 223-8522, Japan email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a non-generic, yet dense subset of 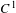$C^{1}$ expanding Markov maps of the interval we prove the existence of uncountably many Lyapunov optimizing measures which are ergodic, fully supported and have positive entropy. These measures are equilibrium states for some Hölder continuous potentials. We also prove the existence of another non-generic dense subset for which the optimizing measure is unique and supported on a periodic orbit. A key ingredient is a new 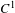$C^{1}$ perturbation theorem which allows us to interpolate between expanding Markov maps and the shift map on a finite number of symbols.

Keywords

expanding Markov mapLyapunov optimizing measurenon-generic property

MSC classification

Primary: 37C40: Smooth ergodic theory, invariant measures 37D35: Thermodynamic formalism, variational principles, equilibrium states 37E05: Maps of the interval (piecewise continuous, continuous, smooth)
Secondary: 37A40: Nonsingular (and infinite-measure preserving) transformations 37D05: Hyperbolic orbits and sets
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2571 - 2592
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baraviera, A., Leplaideur, R. and Lopes, A.. Ergodic optimization, zero temperature limits and the max-plus algebra. 29th Brazilian Mathematics Colloquium (IMPA Mathematical Publications). IMPA, Rio de Janeiro, 2013.Google Scholar
Bousch, T.. Le poisson n’a pas d’arêtes. Ann. Inst. Henri Poincaré Probab. Stat. 36 (2000), 489–508.Google Scholar
Bousch, T.. La condition de Walters. Ann. Sci. Éc. Norm. Supér. 34 (2001), 287–311.Google Scholar
Bousch, T. and Jenkinson, O.. Cohomology classes of dynamically non-negative C k functions. Invent. Math. 148 (2002), 207–217.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory for Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.Google Scholar
Brémont, J.. Gibbs measures at temperature zero. Nonlinearity 16 (2003), 419–426.Google Scholar
Brémont, J.. Entropy and maximizing measures of generic continuous functions. C. R. Math. 346 (2008), 199–201.Google Scholar
Chazottes, J.-R. and Hochman, M.. On the zero-temperature limit of Gibbs states. Comm. Math. Phys. 297 (2010), 265–281.Google Scholar
Contreras, G.. Ground states are generically a periodic orbit. Invent. Math. 205 (2016), 383–412.Google Scholar
Contreras, G., Lopes, A. O. and Thieullen, P.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 21 (2001), 1379–1409.Google Scholar
Coronel, D. and Rivera-Letelier, J.. Sensitive dependence of Gibbs measures at low temperatures. J. Stat. Phys. 160 (2015), 1658–1683.Google Scholar
Hunt, B. and Ott, E.. Optimal periodic orbits of chaotic systems occur at low period. Phys. Rev. E 54 (1996), 328–337.Google Scholar
Hunt, B. and Ott, E.. Optimal periodic orbits of chaotic systems. Phys. Rev. Lett. 76 (1996), 2254–2257.Google Scholar
Israel, R.. Convexity in the Theory of Lattice Gases (Princeton Series in Physics). Princeton University Press, Princeton, NJ, 1979.Google Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. 15 (2006), 197–224.Google Scholar
Jenkinson, O. and Morris, I.. Lyapunov optimizing measures for C 1 expanding maps of the circle. Ergod. Th. & Dynam. Sys. 28 (2008), 1849–1860.Google Scholar
Leplaideur, R.. A dynamical proof for the convergence of Gibbs measures at temperature zero. Nonlinearity 18 (2005), 2847–2880.Google Scholar
Mañé, R.. Generic properties and problems of minimizing measures of Lagrangian systems. Nonlinearity 9 (1996), 273–310.Google Scholar
Mañé, R.. Lagrangian flows: the dynamics of globally minimizing orbits. Bol. Soc. Brasil. Mat. 28 (1997), 141–153.Google Scholar
Mather, J.. Action minimizing invariant measures for positive definite Lagrangian systems. Math. Z. 207 (1991), 169–207.Google Scholar
Morita, T. and Tokunaga, Y.. Measures with maximum total exponent and generic properties of C 1 expanding maps. Hiroshima Math. J. 43 (2013), 351–370.Google Scholar
Quas, A. and Siefken, J.. Ergodic optimization of super-continuous functions on shift spaces. Ergod. Th. & Dynam. Sys. 32 (2012), 2071–2082.Google Scholar
Ruelle, D.. Thermodynamic Formalism: The Mathematical Structures of Equilibrium Statistical Mechanics (Cambridge Mathematical Library), 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Shinoda, M.. Uncountably many maximizing measures for a dense subset of continuous functions. Nonlinearity 31 (2018), 2192–2200.Google Scholar
Sigmund, K.. Generic properties of invariant measures for Axiom A diffeomorphisms. Invent. Math. 11 (1970), 99–109.Google Scholar
Sorrentino, A.. Action-Minimizing Methods in Hamiltonian Dynamics. An Introduction to Aubry–Mather Theory (Mathematical Notes, 50). Princeton University Press, Princeton, NJ, 2015.Google Scholar
Tokunaga, Y.. Measures with maximum total exponent of C 1 -diffeomorphisms with basic sets. Kyushu J. Math. 69 (2015), 95–110.Google Scholar
Yuan, G. and Hunt, B.. Optimal orbits of hyperbolic systems. Nonlinearity 12 (1999), 1207–1224.Google Scholar