Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T04:24:21.917Z Has data issue: false hasContentIssue false
  • English
  • Français

The 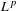$L^{p}$ spectrum and heat dynamics of locally symmetric spaces of higher rank

Published online by Cambridge University Press:  30 June 2014

LIZHEN JI  and
ANDREAS WEBER
LIZHEN JI
Affiliation:
Department of Mathematics, University of Michigan, 1834 East Hall, Ann Arbor, MI 48109-1043, USA email [email protected]
ANDREAS WEBER
Affiliation:
Institut für Algebra und Geometrie, KIT, Kaiserstraße 89–93, 76128 Karlsruhe, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to study the spectrum of the 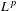$L^{p}$ Laplacian and the dynamics of the 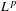$L^{p}$ heat semigroup on non-compact locally symmetric spaces of higher rank. Our work here generalizes previously obtained results in the setting of locally symmetric spaces of rank one to higher rank spaces. Similarly as in the rank-one case, it turns out that the 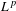$L^{p}$ heat semigroup on 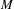$M$ has a certain chaotic behavior if 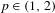$p\in (1,2)$, whereas for 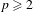$p\geq 2$ such chaotic behavior never occurs.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1524 - 1545
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arendt, W.. Gaussian estimates and interpolation of the spectrum in L p. Differential Integral Equations 7(5–6) (1994), 1153–1168.CrossRefGoogle Scholar
Banasiak, J. and Moszyński, M.. A generalization of Desch–Schappacher–Webb criteria for chaos. Discrete Contin. Dyn. Syst. 12(5) (2005), 959–972.CrossRefGoogle Scholar
Borel, A.. Introduction aux Groupes Arithmétiques (Publications de l’Institut de Mathématique de l’Université de Strasbourg, XV. Actualités Scientifiques et Industrielles, No. 1341). Hermann, Paris, 1969.Google Scholar
Borel, A.. Some metric properties of arithmetic quotients of symmetric spaces and an extension theorem. J. Differential Geom. 6 (1972), 543–560.CrossRefGoogle Scholar
Borel, A.. Stable real cohomology of arithmetic groups. Ann. Sci. Éc. Norm. Supér (4) 7 (1974), 235–272.CrossRefGoogle Scholar
Borel, A. and Ji, L.. Compactifications of Symmetric and Locally Symmetric Spaces (Mathematics: Theory & Applications). Birkhäuser Boston Inc, Boston, MA, 2006.Google Scholar
Davies, E. B.. Pointwise bounds on the space and time derivatives of heat kernels. J. Operator Theory 21(2) (1989), 367–378.Google Scholar
Davies, E. B.. Heat Kernels and Spectral Theory (Cambridge Tracts in Mathematics, 92). Cambridge University Press, Cambridge, 1990.Google Scholar
Davies, E. B.. L p spectral independence and L 1 analyticity. J. Lond. Math. Soc. (2) 52(1) (1995), 177–184.CrossRefGoogle Scholar
Davies, E. B.. L p spectral theory of higher-order elliptic differential operators. Bull. Lond. Math. Soc. 29(5) (1997), 513–546.CrossRefGoogle Scholar
Davies, E. B., Simon, B. and Taylor, M. E.. L p spectral theory of Kleinian groups. J. Funct. Anal. 78(1) (1988), 116–136.CrossRefGoogle Scholar
deLaubenfels, R. and Emamirad, H.. Chaos for functions of discrete and continuous weighted shift operators. Ergod. Th. & Dynam. Sys. 21(5) (2001), 1411–1427.CrossRefGoogle Scholar
Desch, W., Schappacher, W. and Webb, G. F.. Hypercyclic and chaotic semigroups of linear operators. Ergod. Th. & Dynam. Sys. 17(4) (1997), 793–819.CrossRefGoogle Scholar
Devaney, R. L.. An Introduction to Chaotic Dynamical Systems (Addison-Wesley Studies in Nonlinearity). 2nd edn. Addison-Wesley Publishing Company, Redwood City, CA, 1989.Google Scholar
Eberlein, P. B.. Geometry of Nonpositively Curved Manifolds (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 1996.Google Scholar
Gromov, M. and Piatetski-Shapiro, I. I.. Nonarithmetic groups in Lobachevsky spaces. Publ. Math. Inst. Hautes Études Sci. 66 (1988), 93–103.CrossRefGoogle Scholar
Harish-Chandra. Automorphic Forms on Semisimple Lie Groups (Notes by J. G. M. Mars. Lecture Notes in Mathematics, 62). Springer, Berlin, 1968.CrossRefGoogle Scholar
Hempel, R. and Voigt, J.. The spectrum of a Schrödinger operator in L p(R𝜈) is p-independent. Comm. Math. Phys. 104(2) (1986), 243–250.CrossRefGoogle Scholar
Hempel, R. and Voigt, J.. On the L p-spectrum of Schrödinger operators. J. Math. Anal. Appl. 121(1) (1987), 138–159.CrossRefGoogle Scholar
Hieber, M.. Gaussian estimates and invariance of the L p-spectrum for elliptic operators of higher order. Rend. Istit. Mat. Univ. Trieste 28(suppl.) (1997), 235–249.Google Scholar
Ji, L.. The trace class conjecture for arithmetic groups. J. Differential Geom. 48(1) (1998), 165–203.CrossRefGoogle Scholar
Ji, L. and MacPherson, R.. Geometry of compactifications of locally symmetric spaces. Ann. Inst. Fourier (Grenoble) 52(2) (2002), 457–559.CrossRefGoogle Scholar
Ji, L. and Weber, A.. Pointwise bounds for L 2 eigenfunctions on locally symmetric spaces. Ann. Global Anal. Geom. 34(4) (2008), 387–401.CrossRefGoogle Scholar
Ji, L. and Weber, A.. Dynamics of the heat semigroup on symmetric spaces. Ergod. Th. & Dynam. Sys. 30(2) (2010), 457–468.CrossRefGoogle Scholar
Ji, L. and Weber, A.. L p spectral theory and heat dynamics of locally symmetric spaces. J. Funct. Anal. 258 (2010), 1121–1139.CrossRefGoogle Scholar
Ji, L. and Zworski, M.. Scattering matrices and scattering geodesics of locally symmetric spaces. Ann. Sci. Éc. Norm. Supér (4) 34(3) (2001), 441–469.CrossRefGoogle Scholar
Karpelevič, F. I.. The geometry of geodesics and the eigenfunctions of the Beltrami–Laplace operator on symmetric spaces. Trans. Moscow Math. Soc. 1965 (1967), 51–199.Google Scholar
Knapp, A. W.. Representation Theory of Semisimple groups. An Overview Based on Examples (Princeton Landmarks in Mathematics). Princeton University Press, Princeton, NJ, 2001.Google Scholar
Kunstmann, P. C.. Heat kernel estimates and L p spectral independence of elliptic operators. Bull. Lond. Math. Soc. 31(3) (1999), 345–353.CrossRefGoogle Scholar
Kunstmann, P. C.. Uniformly elliptic operators with maximal L p-spectrum in planar domains. Arch. Math. 76(5) (2001), 377–384.CrossRefGoogle Scholar
Langlands, R. P.. On the Functional Equations Satisfied by Eisenstein Series (Lecture Notes in Mathematics, 544). Springer, Berlin, 1976.CrossRefGoogle Scholar
Liskevich, V. A. and Perel’muter, M. A.. Analyticity of sub-Markovian semigroups. Proc. Amer. Math. Soc. 123(4) (1995), 1097–1104.Google Scholar
Margulis, G. A.. Discrete Subgroups of Semisimple Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, 3 [Results in Mathematics and Related Areas, 3], 17). Springer, Berlin, 1991.CrossRefGoogle Scholar
Mœglin, C. and Waldspurger, J.-L.. Spectral Decomposition and Eisenstein Series (Cambridge Tracts in Mathematics, 113). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Muñoz, G., Seoane, J. B. and Weber, A.. Periods of strongly continuous semigroups. Bull. London Math. Soc. 44(3) (2012), 480–488.CrossRefGoogle Scholar
Müller, W.. The trace class conjecture in the theory of automorphic forms. Ann. of Math. (2) 130(3) (1989), 473–529.CrossRefGoogle Scholar
Osborne, M. S. and Warner, G.. The Theory of Eisenstein Systems (Pure and Applied Mathematics, 99). Academic Press Inc. [Harcourt Brace Jovanovich Publishers], New York, 1981.Google Scholar
Stanton, R. J. and Tomas, P. A.. Pointwise inversion of the spherical transform on L p(G∕K), 1 ≤ p < 2. Proc. Amer. Math. Soc. 73(3) (1979), 398–404.Google Scholar
Strichartz, R. S.. Analysis of the Laplacian on the complete Riemannian manifold. J. Funct. Anal. 52(1) (1983), 48–79.CrossRefGoogle Scholar
Sturm, K.-T.. On the L p-spectrum of uniformly elliptic operators on Riemannian manifolds. J. Funct. Anal. 118(2) (1993), 442–453.CrossRefGoogle Scholar
Taylor, M. E.. L p-estimates on functions of the Laplace operator. Duke Math. J. 58(3) (1989), 773–793.CrossRefGoogle Scholar
Varopoulos, N. Th.. Analysis on Lie groups. J. Funct. Anal. 76(2) (1988), 346–410.CrossRefGoogle Scholar
Voigt, J.. The sector of holomorphy for symmetric sub-Markovian semigroups. Functional Analysis (Trier, 1994). de Gruyter, Berlin, 1996, pp. 449–453.Google Scholar
Weber, A.. L p-spectral theory of locally symmetric spaces with ℚ-rank one. Math. Phys. Anal. Geom. 10(2) (2007), 135–154.CrossRefGoogle Scholar
Weber, A.. The L p spectrum of Riemannian products. Arch. Math. (Basel) 90 (2008), 279–283.CrossRefGoogle Scholar
Zimmer, R. J.. Ergodic Theory and Semisimple Groups (Monographs in Mathematics, 81). Birkhäuser, Basel, 1984.CrossRefGoogle Scholar