Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T03:22:21.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Local escape rates for 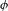$\unicode[STIX]{x1D719}$-mixing dynamical systems

Part of: Ergodic theory

Published online by Cambridge University Press:  25 July 2019

N. HAYDN  and
F. YANG Open the ORCID record for F. YANG [Opens in a new window]
N. HAYDN
Affiliation:
Department of Mathematics, University of Southern California, Los Angeles, CA90089-2532, USA email [email protected]
F. YANG
Affiliation:
Department of Mathematics, University of Oklahoma, Norman, OK73019-3103, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that dynamical systems with $\unicode[STIX]{x1D719}$-mixing measures have local escape rates which are exponential with rate 1 at non-periodic points and equal to the extremal index at periodic points. We apply this result to equilibrium states on subshifts of finite type, Gibbs–Markov systems, expanding interval maps, Gibbs states on conformal repellers, and more generally to Young towers, and by extension to all systems that can be modeled by a Young tower.

Keywords

classical ergodic theorysymbolic dynamicsescape ratesentry times distribution

MSC classification

Primary: 37A25: Ergodicity, mixing, rates of mixing
Secondary: 37A05: Measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 10 , October 2020 , pp. 2854 - 2880
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abadi, M.. Exponential approximation for hitting times in mixing processes. Math. Phys. Electron. J. 7(2) (2001).Google Scholar
Abadi, M.. Sharp error terms and necessary conditions for exponential hitting times in mixing processes. Ann. Probab. 32 (2004), 243–264.CrossRefGoogle Scholar
Abadi, M. and Vergne, N.. Sharp error terms for return time statistics under mixing conditions. J. Theoret. Probab. 22 (2009), 18–37.Google Scholar
Afraimovich, V. S. and Bunimovich, L. A.. Which hole is leaking the most: a topological approach to study open systems. Nonlinearity 23 (2010), 643–656.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States for Anosov Diffeomorphism (Springer Lecture Notes, 470) . Springer, New York, 1975, Second revised edition Springer, Berlin, 2008, available at https://www.cpht.polytechnique.fr/sites/default/files/Bowen_LN_Math_470_second_ed_v2013.pdf.CrossRefGoogle Scholar
Boyarski, A. and Gora, P.. Invariant Measures and Dynamical Systems in One Dimension (Probability and its Applications) . Birkhäuser, Boston, 1997.Google Scholar
Bruin, H., Demers, M. and Todd, M.. Hitting and escaping statistics: mixing, targets and holes. Adv. Math. 328 (2018), 1263–1298.CrossRefGoogle Scholar
Buckley, S. M.. Is the maximal function of a Lipschitz function continuous? Ann. Acad. Sci. Fenn. Math. 24 (1999), 519–528.Google Scholar
Bunimovich, L. A. and Dettmann, C. P.. Peeping at chaos: nondestructive monitoring of chaotic systems by measuring long-time escape rates. Europhys. Lett. 80(4) (2007), #40001, 6.Google Scholar
Bunimovich, L. and Yurchenko, A.. Where to place a hole to achieve a maximal escape rate. Israel J. Math. 182 (2011), 229–252.Google Scholar
Chernov, N. and Van den Bedem, H.. Expanding maps of interval with holes. Ergod. Th. & Dynam. Sys. 22 (2002), 637–654.Google Scholar
Demers, M. and Young, L.-S.. Escape rates and conditionally invariant measures. Nonlinearity 19 (2006), 377–397.CrossRefGoogle Scholar
de Moivre, A.. Doctrine of Chances. London, 1718.Google Scholar
Ferguson, A. and Pollicott, M.. Escape rates for Gibbs measures. Ergod. Th. & Dynam. Sys. 32(3) (2012), 961–988.Google Scholar
Galves, A. and Schmitt, B.. Inequalities for hitting times in mixing dynamical systems. Random Comput. Dynam. 5 (1997), 337–347.Google Scholar
Haydn, N. and Psiloyenis, Y.. Return times distribution for Markov towers with decay of correlations. Nonlinearity 27(6) (2014), 1323–1349.CrossRefGoogle Scholar
Haydn, N. and Vaienti, S.. The distribution of return times near periodic orbits. Probab. Theory Related Fields 144 (2009), 517–542.CrossRefGoogle Scholar
Haydn, N. and Wasilewska, K.. Limiting distribution and error terms for the number of visits to balls in non-uniformly hyperbolic dynamical systems. Discrete Contin. Dyn. Syst. 36(5) (2016), 2585–2611.Google Scholar
Hirata, M.. Poisson law for Axiom A diffeomorphisms. Ergod. Th. & Dynam. Sys. 13 (1993), 533–556.CrossRefGoogle Scholar
Keller, G. and Liverani, C.. Stability of the spectrum for transfer operators. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 28 (1999), 141–152.Google Scholar
Liverani, C. and Maume-Deschamps, V.. Lasota–Yorke maps with holes: conditionally invariant probability measure and invariant probability measures on the survivor set. Ann. Inst. Henri Poincaré Probab. Stat. 39 (2003), 385–412.CrossRefGoogle Scholar
Melbourne, I. and Nicol, M.. Almost sure invariance principle for nonuniformly hyperbolic systems. Commun. Math. Phys. 260 (2005), 131–146.Google Scholar
Pesin, Y. and Weiss, H.. A multifractal analysis of equilibrium measures for conformal expanding maps and Moran-like geometric constructions. J. Stat. Phys. 86(1/2) (1997), 233–275.CrossRefGoogle Scholar
Pitskel, B.. Poisson law for Markov chains. Ergod. Th. & Dynam. Sys. 11 (1991), 501–513.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, New York, 1982.Google Scholar
Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. of Math. (2) 7 (1998), 585–650.CrossRefGoogle Scholar
Young, L.-S.. Recurrence time and rate of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar