Article contents
Limit drift
Published online by Cambridge University Press: 04 July 2016
Abstract
We study the problem of the existence of wild attractors for critical circle coverings with Fibonacci dynamics. This is known to be related to the drift for the corresponding fixed points of renormalization. The fixed point depends only on the order of the critical point 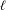 $\ell$ and its drift is a number
$\ell$ and its drift is a number 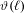 $\unicode[STIX]{x1D717}(\ell )$ which is finite for each finite
$\unicode[STIX]{x1D717}(\ell )$ which is finite for each finite 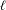 $\ell$. We show that the limit
$\ell$. We show that the limit 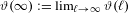 $\unicode[STIX]{x1D717}(\infty ):=\lim _{\ell \rightarrow \infty }\unicode[STIX]{x1D717}(\ell )$ exists and is finite. The finiteness of the limit is in a sharp contrast with the case of Fibonacci unimodal maps. Furthermore,
$\unicode[STIX]{x1D717}(\infty ):=\lim _{\ell \rightarrow \infty }\unicode[STIX]{x1D717}(\ell )$ exists and is finite. The finiteness of the limit is in a sharp contrast with the case of Fibonacci unimodal maps. Furthermore, 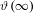 $\unicode[STIX]{x1D717}(\infty )$ is expressed as a contour integral in terms of the limit of the fixed points of renormalization when
$\unicode[STIX]{x1D717}(\infty )$ is expressed as a contour integral in terms of the limit of the fixed points of renormalization when 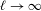 $\ell \rightarrow \infty$. There is a certain paradox here, since this dynamical limit is a circle homeomorphism with the golden mean rotation number whose own drift is
$\ell \rightarrow \infty$. There is a certain paradox here, since this dynamical limit is a circle homeomorphism with the golden mean rotation number whose own drift is 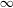 $\infty$ for topological reasons.
$\infty$ for topological reasons.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 2
- Cited by


