Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-10T19:03:29.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Joint ergodicity of actions of an abelian group

Published online by Cambridge University Press:  08 March 2013

YOUNGHWAN SON
YOUNGHWAN SON*
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, Ohio 43210, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 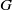$G$ be a countable abelian group and let 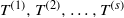${T}^{(1)} , {T}^{(2)} , \ldots , {T}^{(s)} $ be measure preserving $G$-actions on a probability space. We prove that joint ergodicity of 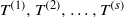${T}^{(1)} , {T}^{(2)} , \ldots , {T}^{(s)} $ implies total joint ergodicity if each 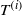${T}^{(i)} $ is totally ergodic. We also show that if 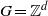$G= { \mathbb{Z} }^{d} $, 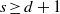$s\geq d+ 1$ and the actions 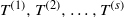${T}^{(1)} , {T}^{(2)} , \ldots , {T}^{(s)} $ commute, then total joint ergodicity of 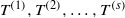${T}^{(1)} , {T}^{(2)} , \ldots , {T}^{(s)} $ follows from joint ergodicity. This can be seen as a generalization of Berend’s result for commuting 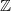$ \mathbb{Z} $-actions.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1353 - 1364
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berend, D.. Joint ergodicity and mixing. J. Anal. Math. 45 (1984), 255–284.Google Scholar
Berend, D.. Multiple ergodic theorems. J. Anal. Math. 50 (1988), 123–142.Google Scholar
Berend, D. and Bergelson, V.. Jointly ergodic measure preserving transformations. Israel J. Math. 49 (1984), 307–314.Google Scholar
Berend, D. and Bergelson, V.. Characterization of joint ergodicity for non-commuting transformations. Israel J. Math. 56 (1986), 123–128.Google Scholar
Bergelson, V., McCutcheon, R. and Zhang, Q.. A Roth theorem for amenable groups. Amer. J. Math. 119 (6) (1997), 1173–1211.CrossRefGoogle Scholar
Bergelson, V. and Rosenblatt, J.. Joint ergodicity for group actions. Ergod. Th. & Dynam. Sys. 8 (1988), 351–364.Google Scholar
Butkevich, S. G.. Convergence of averages in ergodic theory. PhD Dissertation, The Ohio State University, 2000.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.Google Scholar
Krengel, U.. Ergodic Theorems. With a supplement by Antoine Brunel (de Gruyter Studies in Mathematics, 6). Walter de Gruyter, Berlin, 1985.Google Scholar
Nadkarni, M. G.. Basic Ergodic Theory. Birkhäuser, Basel, 1998.Google Scholar
Paterson, A. L. T.. Amenability (Mathematical Surveys and Monographs, 29). American Mathematical Society, Providence, RI, 1988.Google Scholar
de la Rue, T.. An introduction to joinings in ergodic theory. Discrete Contin. Dyn. Syst. 15 (1) (2006), 121–142.Google Scholar
Ryzhikov, V. V.. Joinings, intertwining operators, factors, and mixing properties of dynamical systems. Izv. Math. 42 (1) (1994), 91–113.Google Scholar