Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bergelson, Vitaly
and
Vandehey, Joseph
2019.
A Hot Spot Proof of the Generalized Wall Theorem.
The American Mathematical Monthly,
Vol. 126,
Issue. 10,
p.
876.
Bergelson, Vitaly
Håland Knutson, Inger J
and
Son, Younghwan
2021.
An Extension of Weyl’s Equidistribution Theorem to Generalized Polynomials and Applications.
International Mathematics Research Notices,
Vol. 2021,
Issue. 19,
p.
14965.
Bergelson, Vitaly
Downarowicz, Tomasz
and
Vandehey, Joseph
2022.
Deterministic functions on amenable semigroups and a generalization of the Kamae-Weiss theorem on normality preservation.
Journal d'Analyse Mathématique,
Vol. 148,
Issue. 1,
p.
213.
Bergelson, Vitaly
and
Moragues, Andreu Ferré
2022.
Juxtaposing combinatorial and ergodic properties of large sets of integers.
Israel Journal of Mathematics,
Vol. 251,
Issue. 1,
p.
173.
Cao, Yang
and
Shao, Song
2022.
Topological mild mixing of all orders along polynomials.
Discrete & Continuous Dynamical Systems,
Vol. 42,
Issue. 3,
p.
1163.
Donoso, Sebastián
Koutsogiannis, Andreas
and
Sun, Wenbo
2022.
Seminorms for multiple averages along polynomials and applications to joint ergodicity.
Journal d'Analyse Mathématique,
Vol. 146,
Issue. 1,
p.
1.
Frantzikinakis, Nikos
2023.
Joint ergodicity of sequences.
Advances in Mathematics,
Vol. 417,
Issue. ,
p.
108918.
Bergelson, Vitaly
and
Son, Younghwan
2023.
Joint ergodicity of piecewise monotone interval maps.
Nonlinearity,
Vol. 36,
Issue. 6,
p.
3376.
Bergelson, Vitaly
Moreira, Joel
and
Richter, Florian K.
2024.
Multiple ergodic averages along functions from a Hardy field: Convergence, recurrence and combinatorial applications.
Advances in Mathematics,
Vol. 443,
Issue. ,
p.
109597.
Donoso, Sebastián
Koutsogiannis, Andreas
and
Sun, Wenbo
2025.
Joint ergodicity for functions of polynomial growth.
Israel Journal of Mathematics,
Donoso, Sebastián
Koutsogiannis, Andreas
and
Sun, Wenbo
2025.
Joint transitivity for linear iterates.
Forum of Mathematics, Sigma,
Vol. 13,
Issue. ,
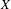 $X$ of the form
$X$ of the form 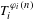 $T_{i}^{\unicode[STIX]{x1D711}_{i}(n)}$ is given for the case where
$T_{i}^{\unicode[STIX]{x1D711}_{i}(n)}$ is given for the case where 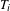 $T_{i}$ are commuting measure-preserving transformations of
$T_{i}$ are commuting measure-preserving transformations of 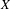 $X$ and
$X$ and 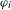 $\unicode[STIX]{x1D711}_{i}$ are integer-valued generalized linear functions, that is, the functions formed from conventional linear functions by an iterated use of addition, multiplication by constants, and the greatest integer function. We also establish a similar criterion for joint ergodicity of families of transformations depending on a continuous parameter, as well as a condition of joint ergodicity of sequences
$\unicode[STIX]{x1D711}_{i}$ are integer-valued generalized linear functions, that is, the functions formed from conventional linear functions by an iterated use of addition, multiplication by constants, and the greatest integer function. We also establish a similar criterion for joint ergodicity of families of transformations depending on a continuous parameter, as well as a condition of joint ergodicity of sequences 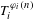 $T_{i}^{\unicode[STIX]{x1D711}_{i}(n)}$ along primes.
$T_{i}^{\unicode[STIX]{x1D711}_{i}(n)}$ along primes.

