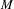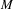Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Neofytidis, Christoforos
2020.
Virtual Betti numbers of mapping tori of 3-manifolds.
Mathematische Zeitschrift,
Vol. 296,
Issue. 3-4,
p.
1691.
Bucher, Michelle
and
Neofytidis, Christoforos
2020.
The simplicial volume of mapping tori of 3-manifolds.
Mathematische Annalen,
Vol. 376,
Issue. 3-4,
p.
1429.