Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-02T02:01:10.001Z Has data issue: false hasContentIssue false
  • English
  • Français

Furstenberg boundaries for pairs of groups

Part of: Noncompact transformation groups Connections with other structures, applications

Published online by Cambridge University Press:  20 February 2020

NICOLAS MONOD Open the ORCID record for NICOLAS MONOD [Opens in a new window]
NICOLAS MONOD*
Affiliation:
EPFL, CH-1015Lausanne, Switzerland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Furstenberg has associated to every topological group 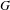$G$ a universal boundary 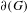$\unicode[STIX]{x2202}(G)$. If we consider in addition a subgroup 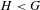$H<G$, the relative notion of 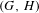$(G,H)$-boundaries admits again a maximal object 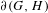$\unicode[STIX]{x2202}(G,H)$. In the case of discrete groups, an equivalent notion was introduced by Bearden and Kalantar (Topological boundaries of unitary representations. Preprint, 2019, arXiv:1901.10937v1) as a very special instance of their constructions. However, the analogous universality does not always hold, even for discrete groups. On the other hand, it does hold in the affine reformulation in terms of convex compact sets, which admits a universal simplex 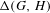$\unicode[STIX]{x1D6E5}(G,H)$, namely the simplex of measures on 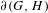$\unicode[STIX]{x2202}(G,H)$. We determine the boundary 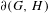$\unicode[STIX]{x2202}(G,H)$ in a number of cases, highlighting properties that might appear unexpected.

Keywords

group actionstopological dynamicsamenability

MSC classification

Primary: 54H20: Topological dynamics
Secondary: 22F05: General theory of group and pseudogroup actions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 5 , May 2021 , pp. 1514 - 1529
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfsen, E. M.. Compact Convex Sets and Boundary Integrals (Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 57) . Springer, New York, 1971.CrossRefGoogle Scholar
Anantharaman-Delaroche, C.. Amenability and exactness for dynamical systems and their C ∗ -algebras. Trans. Amer. Math. Soc. 354(10) (2002), 4153–4178.CrossRefGoogle Scholar
Bauer, H.. Šilovscher Rand und Dirichletsches Problem. Ann. Inst. Fourier (Grenoble) 11 (1961), 89–136, XIV.CrossRefGoogle Scholar
Bearden, A. and Kalantar, M.. Topological boundaries of unitary representations. Preprint, 2019, arXiv: 1901.10937v1.CrossRefGoogle Scholar
Bishop, E. and Leeuw, K. de. The representations of linear functionals by measures on sets of extreme points. Ann. Inst. Fourier (Grenoble) 9 (1959), 305–331.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N.. Relative amenability. Groups Geom. Dyn. 8(3) (2014), 747–774.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J. T.. Linear Operators I. General Theory (Pure and Applied Mathematics, 7) . Interscience Publishers, New York, 1958.Google Scholar
Eymard, P.. Moyennes invariantes et représentations unitaires (Lecture Notes in Mathematics, 300) . Springer, Berlin, 1972.CrossRefGoogle Scholar
Furstenberg, H.. A Poisson formula for semi-simple Lie groups. Ann. of Math. (2) 77 (1963), 335–386.CrossRefGoogle Scholar
Furstenberg, H.. Boundary theory and stochastic processes on homogeneous spaces. Harmonic Analysis on Homogeneous Spaces (Proceedings of Symposia in Pure Mathematics, XXVI) . American Mathematical Society, Providence, RI, 1973, pp. 193–229.CrossRefGoogle Scholar
Glasner, S.. Proximal Flows (Lecture Notes in Mathematics, 517) . Springer, Berlin, 1976.CrossRefGoogle Scholar
Glasner, Y. and Monod, N.. Amenable actions, free products and a fixed point property. Bull. Lond. Math. Soc. 39(1) (2007), 138–150.CrossRefGoogle Scholar
Hart, K. P., Nagata, J.-i. and Vaughan, J. E. (Eds). Encyclopedia of General Topology. Elsevier, Amsterdam, 2004.Google Scholar
la Harpe, P. de. Moyennabilité de quelques groupes topologiques de dimension infinie. C. R. Acad. Sci. Paris Sér. A-B 277 (1973), A1037–A1040.Google Scholar
la Harpe, P. de and Valette, A.. La propriété (T) de Kazhdan pour les groupes localement compacts. Astérisque 175 (1989), with an appendix by M. Burger.Google Scholar
Magnus, W., Karrass, A. and Solitar, D. M.. Combinatorial Group Theory: Presentations of Groups in Terms of Generators and Relations, revised edn. Dover Publications, New York, 1976.Google Scholar
Monod, N.. Gelfand pairs admit an Iwasawa decomposition. Preprint, 2019, arXiv:1902.09497.Google Scholar
Monod, N. and Popa, S.. On co-amenability for groups and von Neumann algebras. C. R. Math. Acad. Sci. Soc. R. Can. 25(3) (2003), 82–87.Google Scholar
Osin, D. V.. Relatively hyperbolic groups: intrinsic geometry, algebraic properties, and algorithmic problems. Mem. Amer. Math. Soc. 179(843) (2006).Google Scholar
Pestov, V. G.. On some questions of Eymard and Bekka concerning amenability of homogeneous spaces and induced representations. C. R. Math. Acad. Sci. Soc. R. Can. 25(3) (2003), 76–81.Google Scholar
Phelps, R. R.. Lectures on Choquet’s Theorem (Lecture Notes in Mathematics, 1757) . 2nd edn. Springer, Berlin, 2001.CrossRefGoogle Scholar
Portmann, J.. Counting integral points on affine homogeneous varieties and Patterson–Sullivan theory. PhD Thesis, ETH Zürich, 2013.Google Scholar
Poulsen, E. T.. A simplex with dense extreme points. Ann. Inst. Fourier. (Grenoble) 11 (1961), 83–87.CrossRefGoogle Scholar
Zucker, A.. Maximally highly proximal flows. Preprint, 2019, arXiv:1812.00392v2.Google Scholar