Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-05T16:01:30.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Flexible periodic points

Published online by Cambridge University Press:  14 March 2014

CHRISTIAN BONATTI  and
KATSUTOSHI SHINOHARA
CHRISTIAN BONATTI
Affiliation:
Institut de Mathématiques de Bourgogne, CNRS – UMR 5584, Université de Bourgogne, 9 av. A. Savary, 21000 Dijon, France email [email protected]
KATSUTOSHI SHINOHARA
Affiliation:
Collaborative Research Center for Innovative Mathematical Modelling, Institute of Industrial Science, The University of Tokyo, 4-6-1-Cw601 Komaba, Meguro-ku, Tokyo, 153-8505, Japan email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define the notion of ${\it\varepsilon}$-flexible periodic point: it is a periodic point with stable index equal to two whose dynamics restricted to the stable direction admits ${\it\varepsilon}$-perturbations both to a homothety and a saddle having an eigenvalue equal to one. We show that an ${\it\varepsilon}$-perturbation to an ${\it\varepsilon}$-flexible point allows us to change it to a stable index one periodic point whose (one-dimensional) stable manifold is an arbitrarily chosen 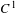$C^{1}$-curve. We also show that the existence of flexible points is a general phenomenon among systems with a robustly non-hyperbolic two-dimensional center-stable bundle.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1394 - 1422
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F., Bonatti, C., Crovisier, S., Díaz, L. J. and Wen, L.. Periodic points and homoclinic classes. Ergod. Th. & Dynam. Sys. 27(1) (2007), 1–22.CrossRefGoogle Scholar
Abraham, R. and Smale, S.. Nongenericity of Ω-stability. Global Analysis (Proc. Symp. Pure Mathematics, Vol. XIV, Berkeley, CA, 1968). American Mathematical Society, Providence, RI, 1970, pp. 5–8.Google Scholar
Bochi, J. and Bonatti, C.. Perturbation of the Lyapunov spectra of periodic orbits. Proc. Lond. Math. Soc. 105(3) (2012), 1–48.CrossRefGoogle Scholar
Bonatti, C.. Survey: towards a global view of dynamical systems, for the C 1-topology. Ergod. Th. & Dynam. Sys. 31(4) (2011), 959–993.CrossRefGoogle Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158(1) (2004), 33–104.CrossRefGoogle Scholar
Bonatti, C., Crovisier, S., Díaz, L. J. and Gourmelon, N.. Internal perturbations of homoclinic classes: non-domination, cycles, and self-replication. Ergod. Th. & Dynam. Sys. 33(3) (2013), 739–776.CrossRefGoogle Scholar
Bonatti, C., Crovisier, S., Vago, G. M. and Wilkinson, A.. Local density of diffeomorphisms with large centralizers. Ann. Sci. Éc. Norm. Supér. (4) 41(6) (2008), 925–954.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J.. On maximal transitive sets of generic diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 96 (2003), 171–197.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J.. Robust heterodimensional cycles and C 1-generic dynamics. J. Inst. Math. Jussieu 7(3) (2008), 469–525.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Kiriki, S.. Stabilization of heterodimensional cycles. Nonlinearity 25(4) (2012), 931–960.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Pujals, E.. A C 1-generic dichotomy for diffeomorphisms: weak forms of hyperbolicity or infinitely many sinks or sources. Ann. of Math. (2) 158(2) (2003), 355–418.CrossRefGoogle Scholar
Bonatti, C., Gourmelon, N. and Vivier, T.. Perturbations of linear cocycles. Ergod. Th. & Dynam. Sys. 26(5) (2006), 1307–1337.CrossRefGoogle Scholar
Bonatti, C. and Shinohara, K.. Flexible points and wild diffeomorphisms. In preparation.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.CrossRefGoogle Scholar
Crovisier, S. and Pujals, E.. Essential hyperbolicity and homoclinic bifurcations: a dichotomy phenomenon/mechanism for diffeomorphisms. Preprint, arXiv:1011.3836.Google Scholar
Franks, J.. Necessary conditions for stability of diffeomorphisms. Trans. Amer. Math. Soc. 158 (1971), 301–308.CrossRefGoogle Scholar
Gourmelon, N.. A Franks’ lemma that preserves invariant manifolds. Preprint, arXiv: 0912.1121.Google Scholar
Gourmelon, N.. Generation of homoclinic tangencies by C 1-perturbations. Discrete Contin. Dyn. Syst. 26(1) (2010), 1–42.CrossRefGoogle Scholar
Hayashi, S.. Connecting invariant manifolds and the solution of the C 1-stability and Ω-stability conjectures for flows. Ann. of Math. (2) 145(1) (1997), 81–137.CrossRefGoogle Scholar
Newhouse, S.. Diffeomorphisms with infinitely many sinks. Topology 13 (1974), 9–18.CrossRefGoogle Scholar
Mañé, R.. An ergodic closing lemma. Ann. of Math. (2) 116(3) (1982), 503–540.CrossRefGoogle Scholar
Pujals, E. R. and Sambarino, M.. Homoclinic tangencies and hyperbolicity for surface diffeomorphisms. Ann. of Math. (2) 151(3) (2000), 961–1023.CrossRefGoogle Scholar
Shinohara, K.. On the index problem of C 1-generic wild homoclinic classes in dimension three. Discrete Contin. Dyn. Syst. 31(3) (2011), 913–940.CrossRefGoogle Scholar
Wen, L.. Homoclinic tangencies and dominated splittings. Nonlinearity 15(5) (2002), 1445–1469.CrossRefGoogle Scholar