Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T00:26:09.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Flexibility of Lyapunov exponents with respect to two classes of measures on the torus

Part of: Ergodic theory Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  31 May 2021

ALENA ERCHENKO
ALENA ERCHENKO*
Affiliation:
Mathematics Department, Stony Brook University, Simons Center for Geometry and Physics, Stony Brook, NY, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a smooth area-preserving Anosov diffeomorphism 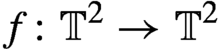$f\colon \mathbb T^2\rightarrow \mathbb T^2$ homotopic to an Anosov automorphism L of 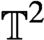$\mathbb T^2$ . It is known that the positive Lyapunov exponent of f with respect to the normalized Lebesgue measure is less than or equal to the topological entropy of L, which, in addition, is less than or equal to the Lyapunov exponent of f with respect to the probability measure of maximal entropy. Moreover, the equalities only occur simultaneously. We show that these are the only restrictions on these two dynamical invariants.

Keywords

flexibilityLyapunov exponentsAnosov diffeomorphismMarkov partitionslow-down deformation

MSC classification

Primary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.) 37A35: Entropy and other invariants, isomorphism, classification
Secondary: 37C05: Smooth mappings and diffeomorphisms 37A05: Measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 2: Anatole Katok Memorial Issue Part 1: Special Issue of Ergodic Theory and Dynamical Systems , February 2022 , pp. 737 - 776
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to Anatole Katok

References

Anosov, D. and Sinai, Y.. Certain smooth ergodic systems. Russian Math. Surveys 22 (1967), 103–167.Google Scholar
Adler, R. and Weiss, B.. Entropy, a complete metric invariant for automorphisms of the torus. Proc. Natl. Acad. Sci. USA 57 (1967), 1573–1576.CrossRefGoogle ScholarPubMed
Burns, K. and Gelfert, K.. Lyapunov spectrum for geodesic flows of rank 1 surfaces. Discrete Contin. Dyn. Syst. 34(5) (2014), 1841–1872.10.3934/dcds.2014.34.1841CrossRefGoogle Scholar
Bochi, J., Katok, A. and Hertz, F. R.. Flexibility of Lyapunov exponents. Ergod. Th. & Dynam. Sys. this special issue.Google Scholar
Bowen, R.. Periodic points and measures for Axiom A diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Barreira, L. and Pesin, Y.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and its Applications, 115). Cambridge University Press, Cambridge, 2007.CrossRefGoogle Scholar
de la Llave, R.. Invariant for smooth conjugacy of hyperbolic dynamical systems II. Comm. Math. Phys. 109 (1987), 369–378.CrossRefGoogle Scholar
Erchenko, A.. Flexibility of Lyapunov exponents for expanding circle maps. Discrete Contin. Dyn. Syst. 39(5) (2019), 2325–2342.CrossRefGoogle Scholar
Hu, H., Jiang, M. and Jiang, Y.. Infimum of the metric entropy of volume preserving Anosov systems. Discrete Contin. Dyn. Syst. 37(9) (2017), 4767–4783.10.3934/dcds.2017205CrossRefGoogle Scholar
Katok, A.. Bernoulli diffeomorphisms on surfaces. Ann. of Math. (2) 110(3) (1979), 529–547.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, Cambridge, 1995. With a supplementary chapter by Katok and L. Mendoza.CrossRefGoogle Scholar
Kotani, M. and Sunada, T.. The pressure and higher correlations for an Anosov diffeomorphism. Ergod. Th. & Dynam. Sys. 21 (2001), 807–821.CrossRefGoogle Scholar
Marco, J. M. and Moriyón, R.. Invariants for smooth conjugacy of hyperbolic dynamical systems, III. Comm. Math. Phys. 112(2) (1987), 317–333.CrossRefGoogle Scholar
Moser, J.. On a theorem of Anosov. J. Differential Equations 5 (1969), 411–440.CrossRefGoogle Scholar
Pesin, Y., Senti, S. and Zhang, K.. Thermodynamics of the Katok map. Ergod. Th. & Dynam. Sys. 39 (2019), 764–794.CrossRefGoogle Scholar
Ruelle, D.. An inequality for the entropy of differentiable maps. Bull. Braz. Math. Soc. 9 (1978), 83–87.CrossRefGoogle Scholar
Ruelle, D.. Thermodynamic Formalism: The Mathematical Structure of Equilibrium Statistical Mechanics (Cambridge Mathematical Library) , 2nd edn. Cambridge University Press, Cambridge, 2004.CrossRefGoogle Scholar