Article contents
Fixed points of nilpotent actions on 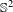 $\mathbb{S}^{2}$
$\mathbb{S}^{2}$
Published online by Cambridge University Press: 05 August 2014
Abstract
We prove that a nilpotent subgroup of orientation-preserving 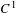 $C^{1}$ diffeomorphisms of
$C^{1}$ diffeomorphisms of 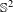 $\mathbb{S}^{2}$ has a finite orbit of cardinality at most two. We also prove that a finitely generated nilpotent subgroup of orientation-preserving
$\mathbb{S}^{2}$ has a finite orbit of cardinality at most two. We also prove that a finitely generated nilpotent subgroup of orientation-preserving 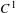 $C^{1}$ diffeomorphisms of
$C^{1}$ diffeomorphisms of 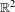 $\mathbb{R}^{2}$ preserving a compact set has a global fixed point. These results generalize theorems of Franks et al for the abelian case. We show that a nilpotent subgroup of orientation-preserving
$\mathbb{R}^{2}$ preserving a compact set has a global fixed point. These results generalize theorems of Franks et al for the abelian case. We show that a nilpotent subgroup of orientation-preserving 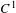 $C^{1}$ diffeomorphisms of
$C^{1}$ diffeomorphisms of 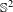 $\mathbb{S}^{2}$ that has a finite orbit of odd cardinality also has a global fixed point. Moreover, we study the properties of the 2-points orbits of nilpotent fixed-point-free subgroups of orientation-preserving
$\mathbb{S}^{2}$ that has a finite orbit of odd cardinality also has a global fixed point. Moreover, we study the properties of the 2-points orbits of nilpotent fixed-point-free subgroups of orientation-preserving 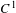 $C^{1}$ diffeomorphisms of
$C^{1}$ diffeomorphisms of 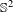 $\mathbb{S}^{2}$.
$\mathbb{S}^{2}$.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 2
- Cited by


