Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-07T07:51:16.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic theorem involving additive and multiplicative groups of a field and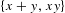$\{x+y,xy\}$ patterns

Published online by Cambridge University Press:  06 October 2015

VITALY BERGELSON  and
JOEL MOREIRA
VITALY BERGELSON
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA email [email protected], [email protected]
JOEL MOREIRA
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish a ‘diagonal’ ergodic theorem involving the additive and multiplicative groups of a countable field 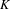$K$ and, with the help of a new variant of Furstenberg’s correspondence principle, prove that any ‘large’ set in 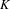$K$ contains many configurations of the form 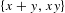$\{x+y,xy\}$. We also show that for any finite coloring of 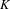$K$ there are many 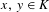$x,y\in K$ such that 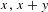$x,x+y$ and 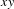$xy$ have the same color. Finally, by utilizing a finitistic version of our main ergodic theorem, we obtain combinatorial results pertaining to finite fields. In particular, we obtain an alternative proof for a result obtained by Cilleruelo [Combinatorial problems in finite fields and Sidon sets. 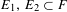Combinatorica32(5) (2012), 497–511], showing that for any finite field $F$ and any subsets $E_{1},E_{2}\subset F$ with 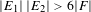$|E_{1}|\,|E_{2}|>6|F|$, there exist 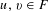$u,v\in F$ such that 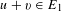$u+v\in E_{1}$ and 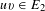$uv\in E_{2}$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 3 , May 2017 , pp. 673 - 692
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arveson, W.. An Invitation to C ∗ -algebras (Graduate Texts in Mathematics, 39) . Springer, New York, 1976, p. 2.CrossRefGoogle Scholar
Beiglböck, M., Bergelson, V., Hindman, N. and Strauss, D.. Multiplicative structures in additively large sets. J. Combin. Theory Ser. A 113(7) (2006), 1219–1242.CrossRefGoogle Scholar
Bergelson, V.. A density statement generalizing Schur’s theorem. J. Combin. Theory Ser. A 43(2) (1986), 338–343.CrossRefGoogle Scholar
Bergelson, V.. Ergodic Ramsey theory—an update. Ergodic Theory of Z d Actions (Warwick, 1993–1994) (London Mathematical Society Lecture Note Series, 228) . Cambridge University Press, Cambridge, 1996, pp. 1–61.Google Scholar
Bergelson, V.. Multiplicatively large sets and ergodic Ramsey theory. Israel J. Math. 148 (2005), 23–40.CrossRefGoogle Scholar
Bergelson, V.. Combinatorial and diophantine applications of ergodic theory. Handbook of Dynamical Systems. 1B. Eds. Hasselblatt, B. and Katok, A.. Elsevier, Amsterdam, 2006, pp. 745–841.CrossRefGoogle Scholar
Bergelson, V.. Ultrafilters, IP sets, dynamics, and combinatorial number theory. Ultrafilters Across Mathematics (Contemporary Mathematics, 530) . American Mathematical Society, Providence, RI, 2010, pp. 23–47.CrossRefGoogle Scholar
Bergelson, V., Furstenberg, H. and McCutcheon, R.. IP-sets and polynomial recurrence. Ergod. Th. & Dynam. Sys. 16(5) (1996), 963–974.CrossRefGoogle Scholar
Bergelson, V., Leibman, A. and McCutcheon, R.. Polynomial Szemerédi theorems for countable modules over integral domains and finite fields. J. Anal. Math. 95 (2005), 243–296.CrossRefGoogle Scholar
Bergelson, V. and McCutcheon, R.. Uniformity in the polynomial Szemerédi theorem. Ergodic Theory of Z d Actions (Warwick, 1993–1994) (London Mathematical Society Lecture Note Series, 228) . Cambridge University Press, Cambridge, 1996, pp. 273–296.Google Scholar
Cilleruelo, J.. Combinatorial problems in finite fields and Sidon sets. Combinatorica 32(5) (2012), 497–511.CrossRefGoogle Scholar
Frantzikinakis, N. and Host, B.. Uniformity of multiplicative functions and partition regularity of some quadratic equations. Preprint, 2013, arXiv:1303.4329.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.CrossRefGoogle Scholar
Hanson, B.. Capturing forms in dense subsets of finite fields. Acta Arith. 160(3) (2013), 277–284.CrossRefGoogle Scholar
Hindman, N.. Monochromatic sums equal to products in ℕ. Integers 11(4) (2011), 431–439.CrossRefGoogle Scholar
Hindman, N., Leader, I. and Strauss, D.. Open problems in partition regularity. Combin. Probab. Comput. 12(5–6) (2003), 571–583; Special issue on Ramsey theory.CrossRefGoogle Scholar
Schur, I.. Über die kongruenz x m + y m = z m (mod p). Jahresber. Dtsch. Math.-Ver. 25 (1916), 114–117.Google Scholar
Shkredov, I. D.. On monochromatic solutions of some nonlinear equations in ℤ/pℤ. Mat. Zametki 88(4) (2010), 625–634.Google Scholar
Stone, M. H.. Applications of the theory of Boolean rings to general topology. Trans. Amer. Math. Soc. 41(3) (1937), 375–481.CrossRefGoogle Scholar