Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T04:12:38.142Z Has data issue: false hasContentIssue false
  • English
  • Français

Endperiodic automorphisms of surfaces and foliations

Part of: Differential topology Low-dimensional dynamical systems

Published online by Cambridge University Press:  07 October 2019

JOHN CANTWELL Open the ORCID record for JOHN CANTWELL [Opens in a new window] ,
LAWRENCE CONLON  and
SERGIO R. FENLEY
JOHN CANTWELL
Affiliation:
Saint Louis University, St. Louis, MO63103, USA email [email protected]
LAWRENCE CONLON
Affiliation:
Washington University, St. Louis, MO63130, USA email [email protected]
SERGIO R. FENLEY
Affiliation:
Florida State University, Tallahassee, FL32306-4510, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the unpublished work of Handel and Miller on the classification, up to isotopy, of endperiodic automorphisms of surfaces. We give the Handel–Miller construction of the geodesic laminations, give an axiomatic theory for pseudo-geodesic laminations, show that the geodesic laminations satisfy the axioms, and prove that pseudo-geodesic laminations satisfying our axioms are ambiently isotopic to the geodesic laminations. The axiomatic approach allows us to show that the given endperiodic automorphism is isotopic to a smooth endperiodic automorphism preserving smooth laminations ambiently isotopic to the original ones. Using the axioms, we also prove the ‘transfer theorem’ for foliations of 3-manifolds, namely that, if two depth-one foliations 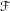${\mathcal{F}}$ and 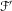${\mathcal{F}}^{\prime }$ are transverse to a common one-dimensional foliation 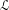${\mathcal{L}}$ whose monodromy on the non-compact leaves of 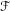${\mathcal{F}}$ exhibits the nice dynamics of Handel–Miller theory, then 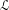${\mathcal{L}}$ also induces monodromy on the non-compact leaves of 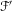${\mathcal{F}}^{\prime }$ exhibiting the same nice dynamics. Our theory also applies to surfaces with infinitely many ends.

Keywords

endperiodiclaminationfinite depth

MSC classification

Primary: 37E30: Homeomorphisms and diffeomorphisms of planes and surfaces
Secondary: 57R30: Foliations; geometric theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 1 , January 2021 , pp. 66 - 212
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altman, I.. The sutured Floer polytope and taut depth-one foliations. Algebr. Geom. Topol. 14 (2014), 1881–1923.Google Scholar
Calegari, D.. Foliations and the Geometry of 3-Manifolds. Oxford University Press, Oxford, 2007.Google Scholar
Candel, A.. Uniformization of surface laminations. Ann. Sci. Éc. Norm. Supér. (4) 26 (1993), 489–516.Google Scholar
Candel, A. and Conlon, L.. Foliations, I. American Mathematical Society, Providence, RI, 1999.Google Scholar
Candel, A. and Conlon, L.. Foliations, II. American Mathematical Society, Providence, RI, 2003.Google Scholar
Cantwell, J. and Conlon, L.. Leaf prescriptions for closed 3-manifolds. Trans. Amer. Math. Soc. 236 (1978), 239–261.Google Scholar
Cantwell, J. and Conlon, L.. Poincaré–Bendixson theory for leaves of codimension one. Trans. Amer. Math. Soc. 265 (1981), 181–209.Google Scholar
Cantwell, J. and Conlon, L.. Tischler fibrations of open foliated sets. Ann. Inst. Fourier (Grenoble) 31 (1981), 113–135.Google Scholar
Cantwell, J. and Conlon, L.. Depth of knots. Topol. Appl. 42 (1991), 277–289.Google Scholar
Cantwell, J. and Conlon, L.. Isotopy of depth one foliations. Proceedings of the International Symposium and Workshop on Geometric Study of Foliations, Tokyo. World Scientific, Singapore, 1994, pp. 153–173.Google Scholar
Cantwell, J. and Conlon, L.. Topological obstructions to smoothing proper foliations. Contemp. Math. 161 (1994), 1–20.Google Scholar
Cantwell, J. and Conlon, L.. Foliation cones. Proceedings of the Kirbyfest (Geometry and Topology Monographs, 2). Geometry and Topology, Coventry, 1999, pp. 35–86.Google Scholar
Cantwell, J. and Conlon, L.. Isotopies of foliated 3-manifolds without holonomy. Adv. Math. 144 (1999), 13–49.Google Scholar
Cantwell, J. and Conlon, L.. Endsets of exceptional leaves; a theorem of G. Duminy. Proceedings of the Euroworkshop on Foliations, Geometry and Dynamics. World Scientific, Singapore, 2002, pp. 225–261.Google Scholar
Cantwell, J. and Conlon, L.. Open saturated sets without holonomy. Preprint, 2011, arXiv:1108.0714v3.Google Scholar
Cantwell, J. and Conlon, L.. Examples of endperiodic automorphisms. Preprint, 2010, arXiv:1008.2549v2.Google Scholar
Cantwell, J. and Conlon, L.. Hyperbolic geometry and homotopic homeomorphisms of surfaces. Geom. Dedicata 177 (2015), 27–42.Google Scholar
Cantwell, J. and Conlon, L.. Cones of foliations almost without holonomy. Geometry, Dynamics, and Foliations 2013 (Advanced Studies in Pure Mathematics, 72). Mathematical Society of Japan, Tokyo, 2017, pp. 301–348.Google Scholar
Casson, A. J. and Bleiler, S. A.. Automorphisms of Surfaces after Nielsen and Thurston. Cambridge University Press, Cambridge, 1988.Google Scholar
Epstein, D. B. A.. Curves on 2-manifolds and isotopies. Acta Math. 115 (1966), 83–107.Google Scholar
Fathi, A., Laudenbach, F. and Poénaru, V.. Travaux de Thurston sur les Surfaces (2ème éd.) (Astérisque, 66–67). Société Mathématique de France, Paris, 1991.Google Scholar
Fenley, S.. Depth one foliations in hyperbolic $3$-manifolds. Thesis, Princeton University, 1990.Google Scholar
Fenley, S.. Asymptotic properties of depth one foliations in hyperbolic 3-manifolds. J. Differential Geom. 36 (1992), 269–313.Google Scholar
Fenley, S.. Endperiodic surface homeomorphisms and 3-manifolds. Math. Z. 224 (1997), 1–24.Google Scholar
Fried, D.. Fibrations over S 1 with pseudo–Anosov monodromy. Travaux de Thurston sur les Surfaces (2ème éd.) (Astérisque, 66–67). Société Mathématique de France, Paris, 1991, pp. 251–266.Google Scholar
Gabai, D.. Foliations and the topology of 3-manifolds. J. Differential. Geom. 18 (1983), 445–503.Google Scholar
Gabai, D.. Foliations and genera of links. Topology 23 (1984), 381–394.Google Scholar
Gabai, D.. Foliations and the topology of 3-manifolds III. J. Differential Geom. 26 (1987), 479–536.Google Scholar
Handel, M. and Thurston, W.. New proofs of some results of Nielson. Adv. Math. 56 (1985), 173–191.Google Scholar
Hatcher, A.. The Kirby torus trick for surfaces. http://www.math.cornell.edu/∼hatcher/Papers/TorusTrick.pdf.Google Scholar
Juhász, A.. The sutured Floer homology polytope. Geom. Topol. 14 (2010), 1303–1354.Google Scholar
Laudenbach, F. and Blank, S.. Isotopie de formes fermées en dimension trois. Inv. Math. 54 (1979), 103–177.Google Scholar
Miller, R. T.. Geodesic laminations from Nielsen’s viewpoint. Adv. Math. 45 (1982), 189–212.Google Scholar
Morgan, J. W. and Shalen, P. B.. Degenerations of hyperbolic structures, II: Measured laminations in 3-manifolds. Ann. Math. 127 (1988), 403–456.Google Scholar
Novikov, S. P.. Topology of foliations. Trans. Moscow Math. Soc. 14 (1965), 268–305.Google Scholar
Pierce, R. S.. Existence and uniqueness theorems for extensions of zero-dimensional compact metric spaces. Trans. Amer. Math. Soc. 148 (1970), 1–21.Google Scholar
Rolfsen, D.. Knots and Links. Publish or Perish, Berkeley, CA, 1976.Google Scholar
Sacksteder, R.. Foliations and pseudogroups. Amer. J. Math. 87 (1965), 79–102.Google Scholar
Schwartzman, S.. Asymptotic cycles. Ann. of Math. (2) 66 (1957), 270–284.Google Scholar
Schweitzer, P.. Counterexamples to the Seifert conjecture and opening closed leaves of foliations. Ann. of Math. (2) 100 (1974), 386–400.Google Scholar
Sullivan, D.. Cycles for the dynamical study of foliated manifolds and complex manifolds. Inv. Math. 36 (1976), 225–255.Google Scholar
Thurston, W.. A norm on the homology of three-manifolds. Mem. Amer. Math. Soc. 59 (1986), 99–130.Google Scholar
Thurston, W.. On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Amer. Math. Soc. 19 (1988), 417–431.Google Scholar
Whitehead, J. H. C.. A certain open manifold whose group is unity. Quart. J. Math. 6 (1936), 268–279.Google Scholar